Frises et isométries
Sommaire
Ce document est une introduction aux frises. C'est un sujet d'application du cours sur les isométries du plan . L'objectif est de faire agir les isométries du plan sur un objet décoratif et de reconnaître les symétries d'une figure.
Pour une étude plus approfondie, consultez Doc Frises et Pavages .
Frises et isométries
Groupe des isométries d'une frise
- Groupe des isométries d'une frise
- Premiers exemples
- Motif d'une frise
- Exemples de mailles et de motifs
- Droite invariante du groupe d'une frise , médiane d'une bande
- Eléments caractéristiques des isométries d'une frise
- Symétries glissées d'une frise
Exercices
- Des exercices italiens.
- Des exercices WIMS.
- Construire une frise invariante par des isométries données. Cliquez sur INTRO/CONFIG pour changer d'isométries.
- Symétries d'une frise
- Choix des éléments de symétrie
- Centres de symétrie d'une frise (dans la deuxième question, il faut cliquer sur tous les centres de symétrie.)
Images de frises
Les frises sont des éléments de décor qu'on retrouve dans de nombreuses civilisations. Leur régularité est due à l'action répétée de certaines isométries du plan sur un motif de base. Contemplez ces exemples pour vous familiariser avec ces objets.
- Une fenêtre sur l'île Saint Louis

Photo Marie-Claude David - Lambroquins à la Réunion
- Sur le site précédent : Frises de tout lieu et tout temps
- Frise obtenue par l'action d'une symétrie glissée et ses composées.

Elle a été construite sur le site italien (voir Construisez votre propre frise ).
Bande et décor
Bande du plan
On suppose désormais choisie une bande du plan. On considère un décor (en couleur) dans la bande, c'est-à-dire une partie de la bande colorée ou non.
Décor dans une bande
Voici un décor dans une bande. Nous incluons ce décor dans une maille (cliquer sur la case maille) et nous construisons une frise (cliquer sur la case frise) . Les définitions de frise et maille sont à la page suivante.Frise, maille
Frise dans une bande
- est un vecteur directeur des deux droites frontières de la bande.
- est invariant par la translation de vecteur , c'est-à-dire : (en tenant compte des couleurs).
- Si est invariant par une translation de vecteur , alors est de la forme , k étant un entier relatif.
Ainsi, est un des deux vecteurs non nuls de norme minimale des translations laissant invariant. On dit que est un vecteur minimal de la frise . On note une frise de vecteur minimal .
On peut exprimer de façon concrète le fait que soit invariant par la translation de vecteur : si on décalque , et si on fait glisser le calque suivant le vecteur , on peut de nouveau faire coïncider le dessin de sur le calque avec .
Maille d'une frise
La frise est l'union des translatés de la maille.
Exemples. Consultez la figure à la page précédente et d'autres exemples ici .
Isométrie d'une frise
On s'intéresse maintenant aux isométries qui conservent (ou laissent invariantes) la frise .
Isométrie de la frise
- l'image de la bande par est égale à la bande
- la frise est invariante par .
Translations de la frise
Notons leur ensemble. L'ensemble est un groupe.
Groupe des isométries d'une frise
Comme on l'observe sur les exemples, le groupe d'une frise reflète les ``symétries'' de la frise (symétries au sens commun). Pour cette raison, il joue un rôle important dans l'étude des frises. Dans la suite, on étudie quelques propriétés des groupes des frises.
- contient l'identité.
- Si g et h sont des isométries de la frise, conserve la frise.
- Si h appartient à , alors appartient à
Pour une étude complète des différents types de groupes de frises, consultez le cours Doc Frises et Pavages .
Premiers exemples
Exemples : Dans l'exemple 1, le groupe est réduit à . Dans l'exemple 2, il contient en plus des symétries centrales.
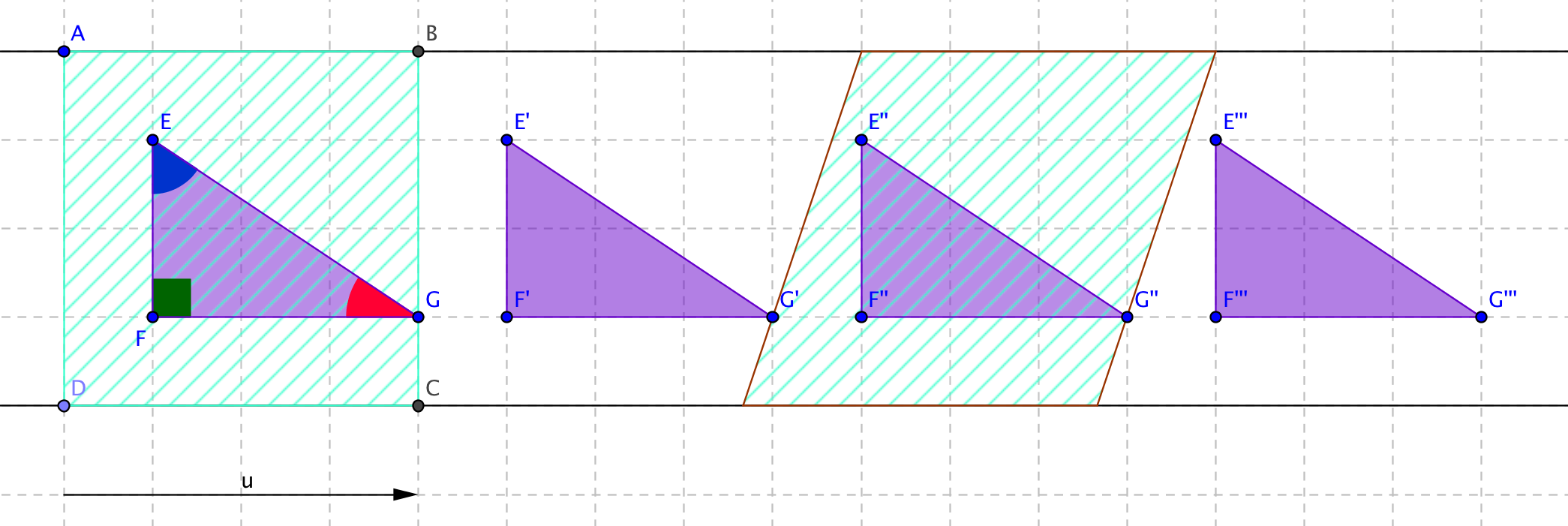
Exemple 1 : Voici une frise de triangles dont le groupe est réduit au groupe des
translations de vecteur
(
).
On a hachuré une maille rectangulaire et une maille parallélogramme.
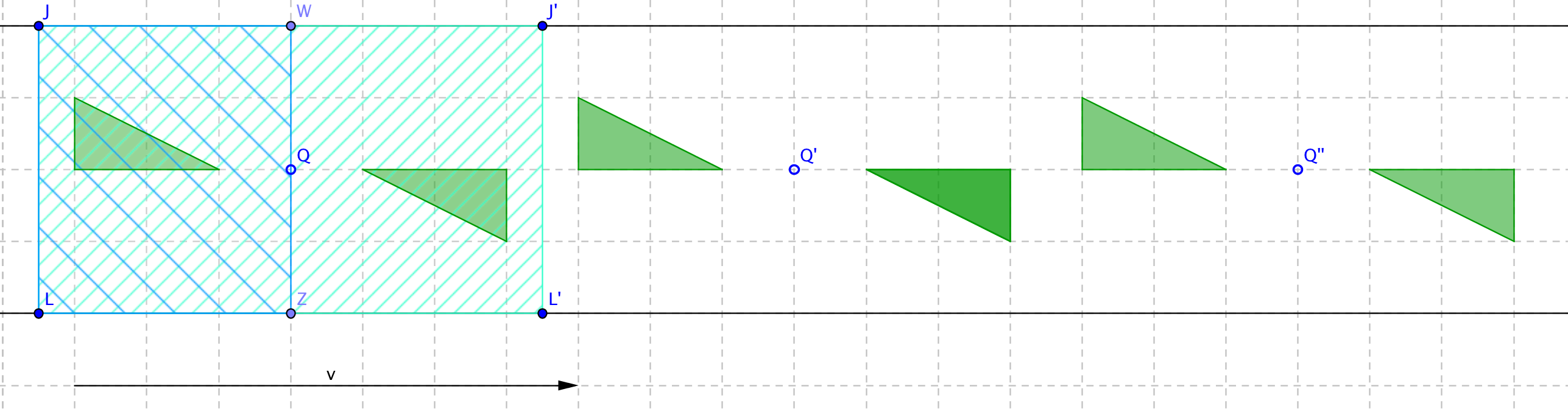
Exemple 2 : Cette frise est invariante par des symétries centrales, par exemple celles
de centre
Q,
Q',
Q''... En voyez-vous d'autres ? Une maille est hachurée une fois ;
un motif qu'elle contient est hachuré deux fois.
Motif d'une frise
Exemples de mailles et de motifs
Une maille est entourée en rouge, un motif est le rectangle à fond clair
Sur un pied : Une maille et un motif sont confondus.
La maille contient les deux pieds, le motif un seul puisque le second s'obtient par isométrie de la frise.
Marche normale
Saut à pieds joints

Danse folklorique

Droite invariante du groupe d'une frise
En effet la frontière de la bande est invariante par toute isométrie de . De plus la médiane est définie par une propriété de distance.

Eléments caractéristiques des isométries d'une frise
Les propriétés d'invariance de la bande et de la médiane permettent de préciser les éléments caractéristiques des isométries de .
- Les centres de symétries de appartiennent à .
- Les axes des réflexions appartenant à sont ou les perpendiculaires à .
- Si contient une symétrie glissée, celle-ci est d'axe et de vecteur , avec .
- Le groupe ne contient aucune rotation qui ne soit ni l'identité, ni une symétrie centrale.
Les résultats nécessaires à cette démonstration sont disponibles dans le cours Isométries du plan .
(1) et (2) résultent des propriétés des droites invariantes par une symétrie centrale ou par une réflexion.
(3) Le carré d'une symétrie glissée qui conserve la frise est une translation qui conserve la frise, donc son vecteur est un multiple de .
(4) résulte de l'absence de droite invariante par une rotation qui n'est ni l'identité, ni une symétrie centrale.
Symétries glissées d'une frise
Nous précisons ici quand le groupe d'une frise contient des symétries glissées et lesquelles.
Si contient , il contient une infinité de symétries glissées ( ).
Si ne contient pas et contient une symétrie glissée, alors il contient la symétrie glissée et ses composées avec les translations.
Construisez votre propre frise
Cette page propose la traduction des consignes d'un exercice en italien. Cet exercice nécessite Java.
Cet exercice interactif propose des motifs pour construire des frises selon des schémas proposés.
Mode d'emploi : Traduction de Istruzioni et de Per saperne di più
En haut, tu as à disposition sept schemas différents pour construire une frise, représentant 7 règles différentes avec lesquelles la figure se répète. Choisis un de ces dessins et puis mets une des formes à disposition dans le rectangle gris clair en bas. Tu peux déplacer une forme en la faisant glisser avec la souris. Quand tu te déplaces sur une forme, celle-ci change de couleur et fait apparaître un point sur un des sommets : si tu cliques sur le point et que tu le traînes tu peux agrandir, faire tourner et réduire la forme.
Quand tu insères une figure dans le rectangle gris clair, une frise apparaît, se répétant suivant un des 7 schémas possibles (celui que tu as choisi au début). La zone gris clair représente le module qui se répète (décoré par les formes que tu as insérées) avec certaines règles (correspondant au schéma choisi) pour former la frise.
Parmi les formes à disposition, il y a aussi un pied : on peut donc aussi essayer de reconstruire 7 façons possibles de procéder qui donnent lieu à 7 frises différentes. Pour chacun des 7 dessins, c'est simple : on peut obtenir par-exemple, au-delà de la marche normale (sixième dessin), le saut à pied joint (premier schéma). Dans les autres cas, il te faudra penser aux façons un peu acrobatiques de procéder.
Tu peux réaliser une frise pour le plaisir ou pour essayer de reproduire une de cette page .
Modèles de frises
Reconnaissez les isométries d'une frise
Cette page propose la traduction des consignes d'un exercice en italien.
Cet exercice en italien permet de déterminer quelle isométrie conserve la frise proposée. On peut travailler sur la frise en photo ou sur les frises dont le motif est le mât du métro. En effet, la page affiche l'image de la frise par l'isométrie testée. Pour la frise en photo, on peut ensuite choisir le type de la frise en cliquant sur les types proposés en-dessous et la correction apparaît à droite de la fiche : "Esatto, è un" signifie "c'est vrai, c'est une" et "No, non è un pm11" signifie " non, ce n'est pas une".
Cette animation utilise Macromedia Flash.
Mode d'emploi : Traduction de Istruzioni
On peut classifier toutes frises selon les 7 types possibles que l'on présente par l'exemple d'un mât du métro. A côté de chaque schéma on trouve les icônes des transformations qui le caractérisent, plus précisément translation,
translation, symétrie centrale
symétrie centrale symétrie glissée,
symétrie glissée, réflexion horizontale
réflexion horizontale réflexion verticale
réflexion verticale
En cliquant sur les icônes de chaque transformation, il est possible d'appliquer à chaque schéma la transformation correspondante, et d'observer son effet sur le schéma choisi. Il est également possible de modifier les paramètres de chaque transformation en utilisant la souris (par exemple, pour les translations on peut modifier la longueur du vecteur, pour les symétries centrales on peut déplacer le centre et ainsi de suite : pour plus de détails, voir la page Pour en savoir plus ).
En haut à gauche on voit la photo d'une frise dont vous devez identifier le type de symétrie. Tout comme pour les schémas de frises, de la même manière, il est possible, en utilisant les boutons correspondant à chaque transformation, d'agir sur la photo pour voir quelles transformations laissent la figure inchangée. Quand vous pensez avoir trouvé le type de symétrie de la frise de la photo, cliquez sur le type correspondant pour savoir si vous avez deviné.
Vous pouvez changer la photo de la frise en cliquant sur [cambia].
Traduction de Per saperne di più
Pour en savoir plus sur le mode d'emploi.
Pour en savoir plus
Ce qui caractérise une frise est le fait qu'une translation la laisse invariante. Il peut ensuite y avoir d'autres transformations la laissant invariante : des réflexions horizontales (par rapport à un axe parallèle à la direction de translation), des réflexions verticales (par rapport à un axe orthogonal à la direction de translation), des réflexions glissées, des symétries centrales. La présence ou non de ces autres transformations dans le groupe de symétrie est vraiment ce qui distingue entre eux les sept types de symétrie d'une frise.
Comment tester l'action d'une isométrie sur un schéma ou une photo (appelés figure dans la suite)
Pour tester une translation, il faut tracer un vecteur : quand tu cliques sur le bouton  , à la figure se superpose une autre copie plus pâle de cette figure, représentant l'effet de la translation relative à ce vecteur. Tu peux modifier la longueur du vecteur avec la souris : on modifie alors la translation et en général les deux figures ne se superposent plus, même si tu peux trouver d'autres longueurs de flèche pour lesquelles les figures se superposent exactement.
, à la figure se superpose une autre copie plus pâle de cette figure, représentant l'effet de la translation relative à ce vecteur. Tu peux modifier la longueur du vecteur avec la souris : on modifie alors la translation et en général les deux figures ne se superposent plus, même si tu peux trouver d'autres longueurs de flèche pour lesquelles les figures se superposent exactement.
Pour détecter une réflexion, il faut tracer une droite : quand tu cliques sur l'un des boutons où figure une droite  ou
ou  , à la figure se superpose une autre copie plus pâle du même dessin, représentant l'effet sur la figure de la réflexion par rapport à cette droite. Tu peux saisir la droite avec la souris et la déplacer, en la maintenant parallèle (respectivement perpendiculaire) à la direction de translation. Quand la position est telle que la figure pâle se superpose exactement à la figure initiale, tu as mis en évidence un axe de symétrie de la figure. Il y a un seul axe de symétrie dans le type p1m1, alors qu'il y en a beaucoup dans le type du pm11.
, à la figure se superpose une autre copie plus pâle du même dessin, représentant l'effet sur la figure de la réflexion par rapport à cette droite. Tu peux saisir la droite avec la souris et la déplacer, en la maintenant parallèle (respectivement perpendiculaire) à la direction de translation. Quand la position est telle que la figure pâle se superpose exactement à la figure initiale, tu as mis en évidence un axe de symétrie de la figure. Il y a un seul axe de symétrie dans le type p1m1, alors qu'il y en a beaucoup dans le type du pm11.
Pour détecter une symétrie glissée, il faut tracer une droite et un vecteur parallèle à cette droite : quand tu cliques sur le bouton  , apparaît comme d'habitude la copie plus pâle avec l'effet de la transformation correspondante. Avec la souris, il est possible de faire varier la longueur du vecteur et d'observer comment varie la symétrie glissée : de nouveau quand la figure pâle se superpose exactement au dessin initial, tu as trouvé une transformation fixant la figure.
, apparaît comme d'habitude la copie plus pâle avec l'effet de la transformation correspondante. Avec la souris, il est possible de faire varier la longueur du vecteur et d'observer comment varie la symétrie glissée : de nouveau quand la figure pâle se superpose exactement au dessin initial, tu as trouvé une transformation fixant la figure.
Enfin, pour une symétrie centrale, il faut fixer un point : quand tu cliques sur le bouton o , la copie pâle et l'effet de la symétrie apparaissent comme d'habitude. Tu peux saisir et déplacer le point avec la souris. Quand la position du point est telle que la figure pâle se superpose exactement à la frise initiale, tu as mis en évidence un centre de symétrie.
, la copie pâle et l'effet de la symétrie apparaissent comme d'habitude. Tu peux saisir et déplacer le point avec la souris. Quand la position du point est telle que la figure pâle se superpose exactement à la frise initiale, tu as mis en évidence un centre de symétrie.
Correction
Pour les sept exemples, seuls les boutons correspondants aux transformations présentes dans le groupe des isométries correspondant sont présentés. Quand tu déplaces les éléments mobiles, ceux-ci changent de couleur aux moments où tu atteins une position pour laquelle la transformation conserve la figure.
Pour la photo, tous les boutons sont présents et c'est à toi de comprendre lesquels correspondent à une transformation fixant la figure et lesquels n'y correspondent pas: quand tu l'as trouvé, l'élément mobile change de couleur et un ok apparaît aux côtés du bouton. Quand tu as trouvé tous les ok de cette photo, tu as tous les éléments pour déterminer de quel type il s'agit.



