DOC Polygones convexes réguliers
Sommaire
Ce document rédigé pour les étudiants de la licence scientifique générale (L3 pour des futurs professeurs des écoles à l'université Paris-Sud) accompagne une partie du cours de géométrie basé sur l'ouvrage de Daniel Perrin : Mathématiques d'école : nombres, mesures et géométrie publié par Editions Cassini (402 p. ISBN 978-2-84225-158-1) . On y fait référence par ME.
ME exercice 187, 185 renvoie à l'exercice 187 de la nouvelle édition, 185 de la première. De même pour les pages ou les propositions.
ME VI.1. renvoie à la partie 1 du chapitre 6.
Polygones convexes réguliers
- Théorème et définition (voir ME V.2.1)
- Propriétés métriques
- Polygones constructibles à la règle et au compas , en particulier
Tronquer un polygone
Il est question ici de construire un polygone régulier inscrit dans un autre, construction utile pour les polyèdres semi-réguliers.- Problèmes , liens avec les polyèdres, résultats généraux, diverses constructions.
- Cas particuliers
Polygones réguliers et aire du disque
Dans cette partie, on utilise des polygones convexes réguliers pour approcher l'aire du disque. On propose des figures pour illustrer la partie longueur du cercle, aire du disque en [ME. VII.4] .
Exercices
Théorème et définition
Cette partie revient sur le Théorème - définition [ME.V.2.1] et en donne une démonstration légèrement différente.Soit un polygone convexe à n côtés. Les propriétés suivantes sont équivalentes :
- Tous les côtés de sont égaux et tous ses angles sont égaux.
- Tous les côtés de sont égaux et tous ses sommets sont sur un cercle.
- Tous les sommets de sont sur un cercle et les angles au centre sont égaux.
Un polygone qui vérifie (3) est invariant par la rotation de centre O et d'angle , c'est pourquoi, on appelle régulier un polygone vérifiant ces propriétés équivalentes du théorème.
Le cercle de centre O passant par les sommets du polygone est appelé cercle circonscrit à . Son centre O est appelé centre de .
Remarque importante où on voit que deux propriétés sont nécessaires à un polygone pour être régulier.
Démonstration du théorème-définition
avec les cas d'isométries (voir cette
page
du Doc Droites remarquables, transformations.)
En [ME.V.2.1], on trouvera aussi une démonstration par les transformations.
Remarque importante
Chaque propriété caractéristique d'un polygone régulier est composée de deux affirmations.
On ne peut les grouper au hasard.
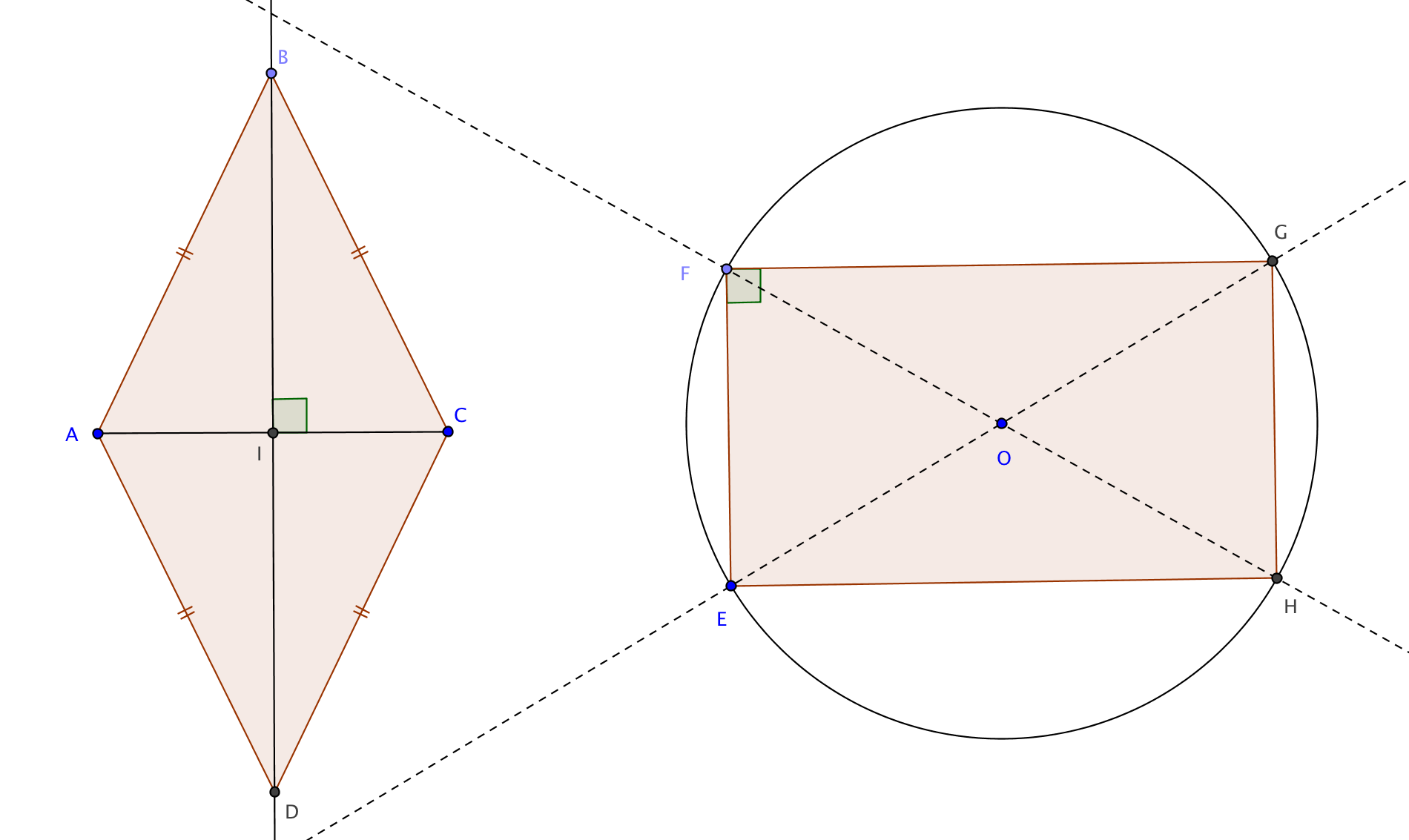
Par exemple, un rectangle non carré a ses sommets cocycliques et ses angles égaux
mais il n'est pas régulier
(ses côtés ne sont pas égaux). Un losange non carré a ses côtés égaux et les angles en son centre égaux
mais il n'est pas régulier (ses sommets ne sont pas cocycliques).
Démonstration du théorème-définition
Pour revoir l'énoncé du théorème, cliquer sur sup.Démonstration de "(1) implique (2)"
Figure 1 : Cette figure présente la démonstration de "(1) implique (2)" par étape. ( Version imprimable de la figure 1 )
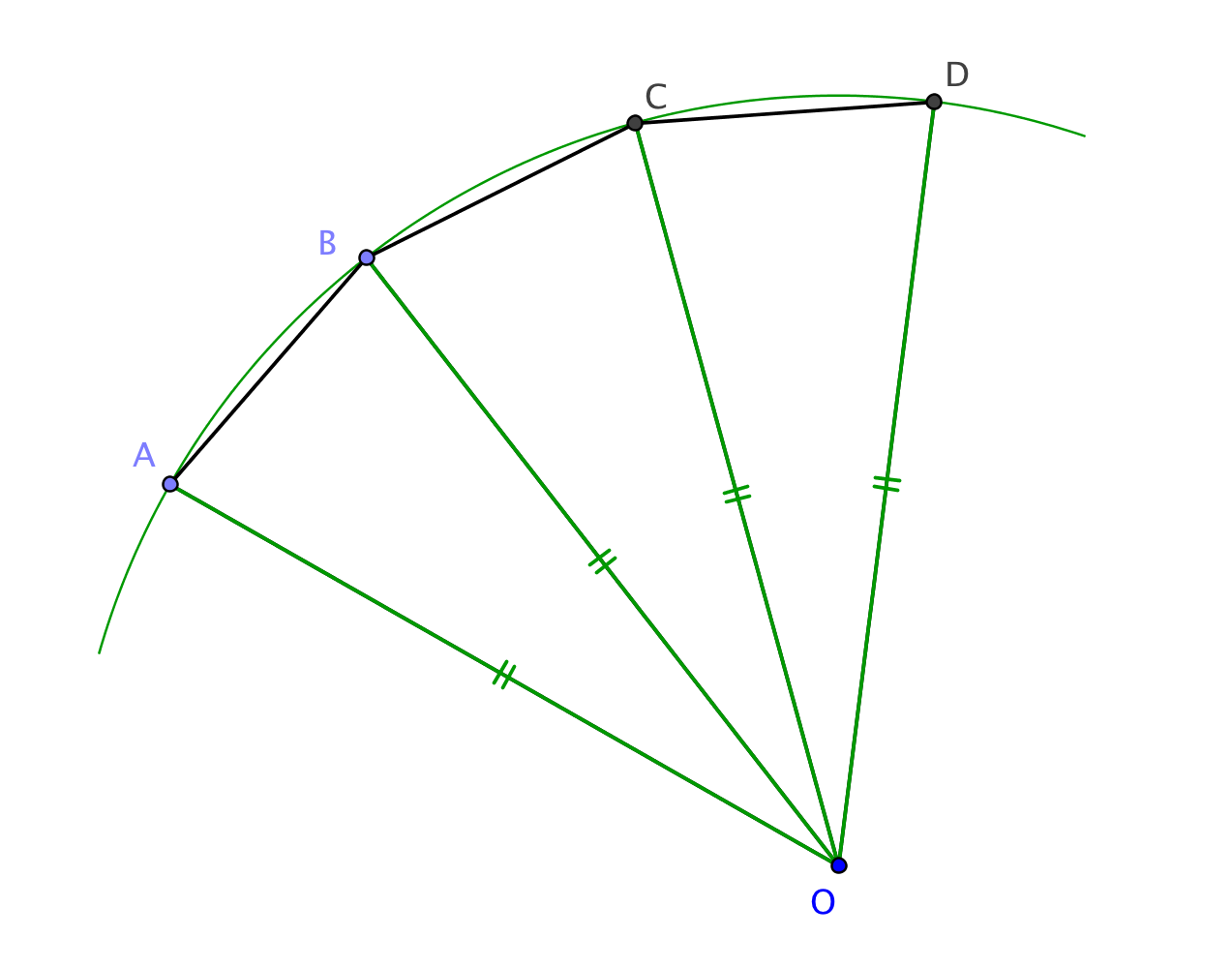
Soit un polygone convexe dont les côtés et les angles sont égaux. Considérons trois sommets A, B et C. On va montrer que le sommet suivant D est sur le cercle circonscrit à A B C.- Commençons par placer D avec les conditions C D = C B et . Deux positions D et D' sont possibles avec ces seules conditions. Or, comme le polygone est convexe, le point D doit être du même côté de (B C) que A, donc une seule position est possible.
- Soit O le centre du cercle circonscrit à ABC, on a alors : O A = O B = O C. De plus par hypothèse, les côtés [A B] et [B C] ont même longueur, les triangles A O B et B O C sont donc isocèles et isométriques par le 3ème cas.
- On en déduit l'égalité des angles à la base des triangles : et comme et sont égaux, on a aussi : par relation de Chasles.
- Alors O B C et O C D sont isométriques par le premier cas. On rappelle que, par hypothèse, les côtés [B C] et [C D] ont même longueur. On en déduit l'égalité : O C = C D donc D appartient au cercle circonscrit à A B C.
Figure 2 : Figure pour la suite. ( Version imprimable de la figure 2 )
Démonstration de "(2) implique (3)"
Si on suppose que tous les sommets sont cocycliques sur un cercle de centre O et les côtés égaux, alors les triangles A O B et B O C sont isométriques par le 3ème cas donc les angles au centre et sont égaux ; on a montré "(2) implique (3)".Démonstration de "(3) implique (1)"
Si on suppose que tous les sommets sont cocycliques sur un cercle de centre O et les angles au centre égaux, alors les triangles A O B, B O C et C O D sont isocèles et isométriques par le premier cas donc les angles et sont égaux ; on a montré "(3) implique (1)".Version imprimable de la figure 1
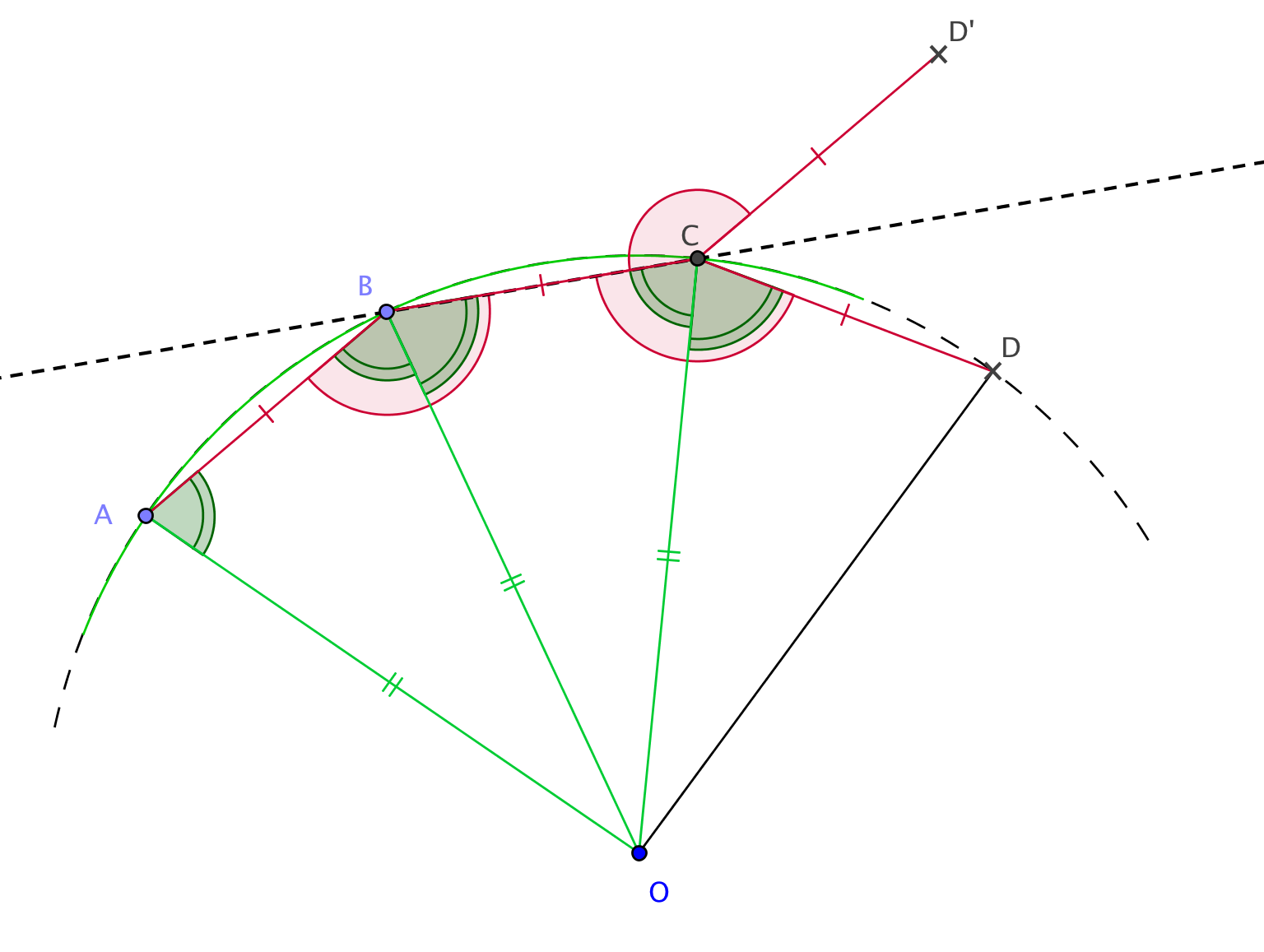
Figure 2
Cette figure illustre la démonstration de "2 implique 3" et "3 implique 1". Dans chaque cas, les points sont cocycliques par hypothèse.
Cochez les cases correspondant aux propriétés que vous supposez vraies et utilisez un cas d'isométrie pour démontrer les autres.
Version imprimable de la figure 2
Propriétés métriques
Les propriétés métriques d'un polygone régulier sont utiles pour les constructions à la règle et au compas et la troncature.Soit un polygone régulier convexe à n côtés, de centre O et soit R le rayon de son cercle circonscrit. On pose Soit Mi le milieu du côté . Pour tout , on a les propriétés suivantes :
- Les angles de sont tous égaux à
- Les angles au centre sont tous égaux à
- Les côtés de ont pour longueur
- Les distances O Mi sont égales à
- L'aire de est égale à Le périmètre p de est égal à On a :
La démonstration repose sur la définition d'un polygone régulier pour (1) et (2), et sur les relations trigonométriques dans le triangle rectangle O Mi Ai pour la suite.
Polygones constructibles à la règle et au compas
Cette partie présente un résumé des résultats concernant la construction à la règle et au compas des polygones convexes réguliers (problème qui agitait déjà les mathématiciens grecs). A quoi cela sert-il ?Résultats généraux
- [ME VI introduction] : Historique.
- [ME VI.1.a] : Principes de la construction à la règle et au compas (voir aussi cette page du Doc Droites remarquables, transformations.)
- [ME VI.2.i] : Résultats généraux concernant la construction des polygones, en particulier 2.20 et 2.21.
Polygones à n côtés ( n ≤ 20)
- Triangle équilatéral
- Etant donné deux points A et B, les points C tel que ABC soit équilatéral sont les points d'intersection des cercles centrés en A et B et de rayon AB.
-
Construction dans un cercle.
Soit
 un cercle de centre
O. On se donne
A un point de
un cercle de centre
O. On se donne
A un point de
 et on note
A′ son symétrique par
rapport à
O c’est-à-dire que
[AA'] est un diamètre de
et on note
A′ son symétrique par
rapport à
O c’est-à-dire que
[AA'] est un diamètre de
 .
On cherche à construire un triangle équilatéral
ABC inscrit dans
.
On cherche à construire un triangle équilatéral
ABC inscrit dans
 .
.
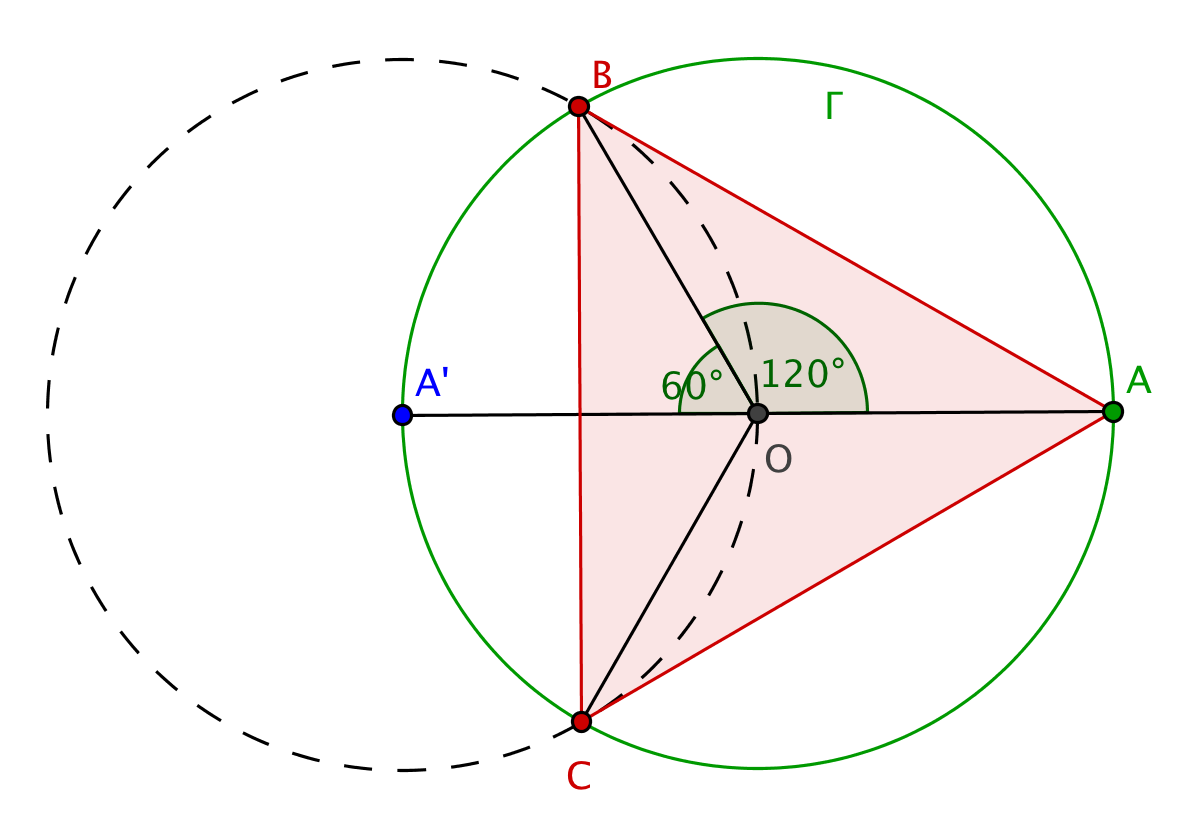
Analyse : Le triangle ABC est équilatéral si et seulement si ses angles au centre et valent si et seulement si les triangles A′ OB et A′ OC sont équilatéraux (triangles isocèles avec un angle de ). Les longueurs A′ B et A′C sont donc égales à A'O.
Construction : Les points B et C sont les intersections de et de
. La construction
est faite en 3 pas à partir de
et de
. La construction
est faite en 3 pas à partir de
 et
A.
et
A.
- Carré
- Pentagone : constructible (voir [ME VI.2.j]) et variantes de la construction.
- Hexagone :
constructible
Soit
 un cercle de centre
O. On se donne
A un point de
un cercle de centre
O. On se donne
A un point de
 et on note
A′ son symétrique par
rapport à
O c'est-à-dire que
[A A'] est un diamètre de
et on note
A′ son symétrique par
rapport à
O c'est-à-dire que
[A A'] est un diamètre de
 .
On cherche à construire un hexagone régulier
A B C D E F inscrit dans
.
On cherche à construire un hexagone régulier
A B C D E F inscrit dans
 .
.
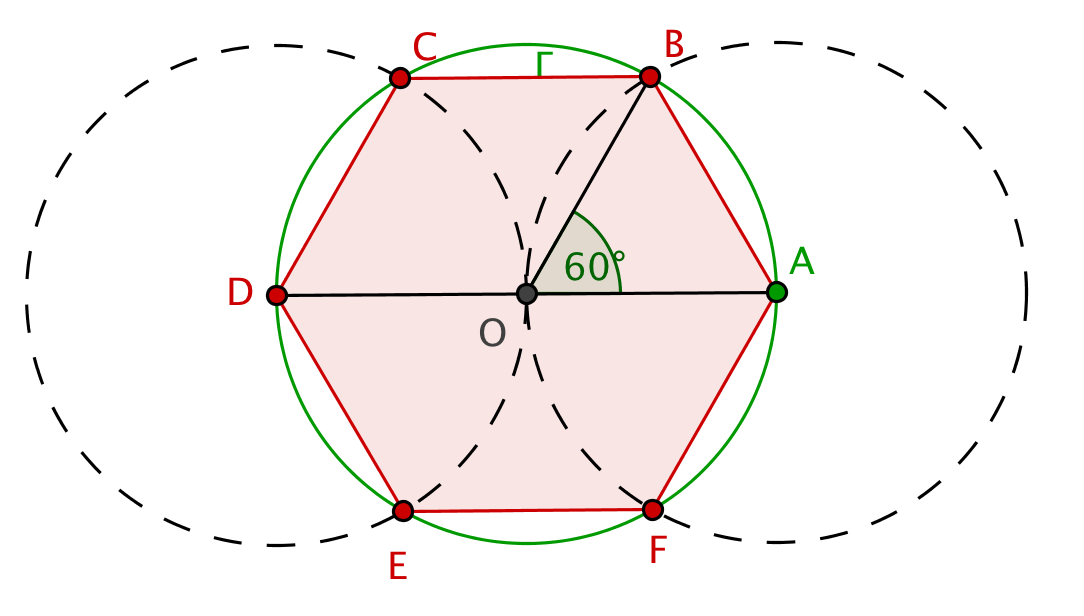
Analyse : D’après la formule du cours, le côté d’un hexagone régulier A B C D E F inscrit dans
 a pour longueur
O A. Ce résultat se montre directement en remarquant que le triangle
A O B est
isocèle avec un angle
de
(angle au centre d’un hexagone régulier).
a pour longueur
O A. Ce résultat se montre directement en remarquant que le triangle
A O B est
isocèle avec un angle
de
(angle au centre d’un hexagone régulier).
Construction : Le point D est confondu avec A′ (l'angle vaut .) Les points B et F sont les intersections de et de
. Les points
C et
E sont les intersections de
et de
. Les points
C et
E sont les intersections de
 et de
La construction est faite en 5 pas à partir de
et de
La construction est faite en 5 pas à partir de
 et
A.
et
A.
L'avantage de cette construction est de minimiser les erreurs de report et de proposer une figure symétrique par rapport à (A D).
- Heptagone : Une construction approchée est proposée dans [ME exercice 176, 175]. L'impossibilité de la construction à la règle et au compas de l'heptagone est l'objet de [ME exercice 187, 185].
- Octogone : constructible à partir d'un carré inscrit dans un cercle et de bissectrices
- Ennéagone ou nonagone : non constructible (voir [ME exercice 186, 184]), construction approchée (voir [ME exercice 180, 178]).
- Décagone : constructible à partir du pentagone et de bissectrices
- Polygone à 11 côtés : non constructible
- Dodécagone : construction avec des bissectrices dans un hexagone (voir aussi [ME exercice 157, 155]).
- Polygone à 13 côtés : non constructible
- Polygone à 14 côtés : non constructible
- Polygone à 15 côtés : construction à partir du triangle équilatéral et du pentagone régulier inscrits dans un cercle (voir [ME exercice 172, 170]).
- Polygone à 16 côtés : construction à partir d'un octogone inscrit dans un cercle et de bissectrices
- Polygone à 17 côtés : constructible
- Polygones à 18 et 19 côtés : non constructibles
- Icosagone : constructible à partir du décagone et de bissectrices
Construction d'un pentagone régulier
Jouez sur la largeur de la fenêtre pour obtenir une mise en page correcte.
Il existe de nombreuses autres constructions que celles proposées ici. Mais toutes reposent sur la construction du nombre puisque l'angle au centre du pentagone régulier est .
Préliminaires
Soient un cercle de centre
O,
[A A'] un diamètre de
un cercle de centre
O,
[A A'] un diamètre de
 et
P un point du cercle tel que
(OP) soit perpendiculaire à
(A A').
On note
H le milieu de
[A'O]. Le triangle
H O P rectangle en
O a pour hypothénuse
[H P] de longueur
.
Alors le cercle de centre
H passant par
P rencontre
[OA] en
Q tel que
donc
OQ vaut
.
et
P un point du cercle tel que
(OP) soit perpendiculaire à
(A A').
On note
H le milieu de
[A'O]. Le triangle
H O P rectangle en
O a pour hypothénuse
[H P] de longueur
.
Alors le cercle de centre
H passant par
P rencontre
[OA] en
Q tel que
donc
OQ vaut
.
Première construction
On renvoie à [ME.VI.2.j] pour le calcul de et une première construction du pentagone régulier.Deuxième construction

Analyse : Le point
I tel que
est donc le milieu de
[O Q].
Les points
B et
E sont les points d'intersection de
 et de la médiatrice de
[O Q].
et de la médiatrice de
[O Q].
Construction : Etant donné le cercle
 et le point
A,
on construit
A', l'autre intersection de
(O A) avec
et le point
A,
on construit
A', l'autre intersection de
(O A) avec
 ,
puis
P comme l'une des intersections de la médiatrice de
[A A'] et de
,
puis
P comme l'une des intersections de la médiatrice de
[A A'] et de
 , puis le milieu
H de
[A'O],
Q intersection du cercle de centre
H passant par
P et de
[O A).
Pour finir les intersections de la médiatrice de
[O Q] avec le cercle
, puis le milieu
H de
[A'O],
Q intersection du cercle de centre
H passant par
P et de
[O A).
Pour finir les intersections de la médiatrice de
[O Q] avec le cercle
 sont les sommets
B et
E.
Les sommets
C et
D s'obtiennent à l'aide des cercles centrés en
B et
E de rayon
A B.
sont les sommets
B et
E.
Les sommets
C et
D s'obtiennent à l'aide des cercles centrés en
B et
E de rayon
A B.
Troisième construction

Analyse : Comme
B est sur la médiatrice de
[O Q],
le triangle
OBQ est isocèle, donc
égale l'angle au centre
du pentagone soit
.
L'angle inscrit
vaut
comme moitié de l'angle au centre
(ou bien par le calcul de la somme des angles dans le triangle isocèle
A'O B). Le triangle
A A'B est donc isocèle car ses angles à la base sont égaux
(la somme des angles d'un triangle vaut
 ). On en déduit que le cercle de centre
A' passant par
Q coupe
). On en déduit que le cercle de centre
A' passant par
Q coupe
 en
B et
E.
en
B et
E.
Construction : Etant donné le cercle
 et le point
A, on construit
A', la médiatrice de
[A A'] pour obtenir
P, le milieu
H de
[A'O],
puis le cercle de centre
H passant par
P pour obtenir
Q et le cercle de centre
A' passant par
Q qui donne
B et
E par intersection avec le cercle
et le point
A, on construit
A', la médiatrice de
[A A'] pour obtenir
P, le milieu
H de
[A'O],
puis le cercle de centre
H passant par
P pour obtenir
Q et le cercle de centre
A' passant par
Q qui donne
B et
E par intersection avec le cercle
 .
Les sommets
C et
D s'obtiennent en reportant la longueur
A B.
.
Les sommets
C et
D s'obtiennent en reportant la longueur
A B.
Tronquer un polygone
Problèmes
- Soit un polygone régulier à n côtés, le polyèdre dont les sommets sont les milieux des côtés de est encore un polygone régulier à n côtés.
-
Le but de cette partie est de construire un polygone régulier
à
2n côtés
dont les sommets sont sur les côtés de
.
- Si n égale 3, c'est facile, il suffit de prendre les sommets de l'hexagone au tiers des côtés du triangle équilatéral (voir Hexagone dans un triangle ).
- Quand n égale 4, ce n'est plus si simple mais c'est encore facile (voir Octogone dans un carré ).
Ces questions surgissent dans la construction des polyèdres archimédiens rectifiés ou tronqués (voir Doc Polyèdres convexes semi-réguliers ).
Premières propriétés
On note A, B, C, ... les sommets de et A′, B′, C′ ... ceux de , M le milieu de [A B], N celui de [B C]. Commençons par deux remarques importantes :- Les polygones et ont le même cercle inscrit, en effet un côté sur deux de est porté par un côté de . On notera O le centre commun des deux polygones.
- Si on a construit un sommet A′ de , on obtient les autres sommets de comme intersections du cercle de centre O passant par A′ avec les côtés de
Constructions
Au moins trois constructions du sommet A′ sont possibles.- avec les longueurs
- avec une bissectrice
- avec un second polygone (en particulier Construction d'un décagone régulier dans un pentagone )
Construction d'un hexagone régulier dans un triangle équilatéral
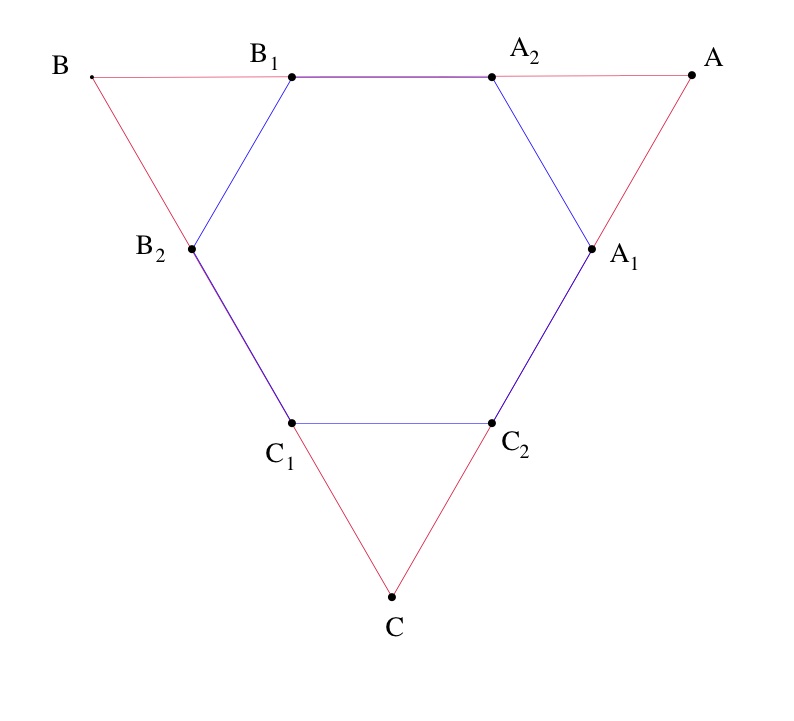
- A2 et B1 sur [AB] tels que
- B2 et C1 sur [BC] tels que
- C2 et A1 sur [CA] tels que
Par hypothèse, le triangle A1 A A2 est isocèle en A et comme A B C est équilatéral, l'angle en A vaut donc A1 A A2 est un triangle équilatéral. De même pour les triangles B1 B B2 et C1 C C2. Donc les côtés de l'hexagone A1 A2 B1 B2 C1 C2 ont tous pour longueur . D'autre part tous ses angles sont supplémentaires d'un angle d'un petit triangle équilatéral donc ils valent tous . L'hexagone A1 A2 B1 B2 C1 C2 a tous ses côtés et ses angles égaux, il est régulier.
Construction d'un octogone régulier dans un carré
Dans le cas n = 4, les formules donnent et . On peut aussi calculer ces valeurs directement en utilisant les relations : c = 2d+c' et (obtenue dans le triangle isocèle rectangle A1 A A2). Ces valeurs nous assurent que les côtés de l'octogone ont même longueur. L'égalité des angles est évidente puisque les triangles "aux coins" du carré sont isocèles rectangles.Construction : Comme vaut , on construit le point B1 comme intersection de [A B] et du cercle centré en A et passant par O. Les autres sommets sont sur le cercle de centre O passant par B1.

Longueur de l'arête de Q'
Analyse
Soit un polygone régulier à n côtés, supposons qu'on ait construit un polygone régulier à 2n côtés dont les sommets sont sur les côtés de . La distance d entre un sommet de et un sommet voisin de dépend de la valeur de n. Grâce aux Propriétés métriques , nous pouvons montrer le résultat général suivant :Démonstration : Dans un polygone régulier à n côtés dont le côté a pour longueur c, on note R le rayon du cercle circonscrit et r le rayon du cercle inscrit. On a : et . On en déduit :
Exemples : Pour n=3, la distance d vaut , pour n=4, elle vaut .
Synthèse
Soit A' placé sur [A B] à la distance d du sommet A de . On doit montrer que les points d'intersection du cercle de centre O passant par A' et des côtés de sont bien les sommets d'un polyèdre régulier. Ils sont cocycliques par construction, il suffit de montrer que tous les côtés de ont même longueur. Par construction et symétrie, les côtés de portés par ceux de de ont pour longueur c'. On conclut en considérant des triangles isocèles et en utilisant des formules métriques dans ces triangles.La synthèse est plus simple pour les cas particuliers qui nous intéressent :
Construction avec une bissectrice
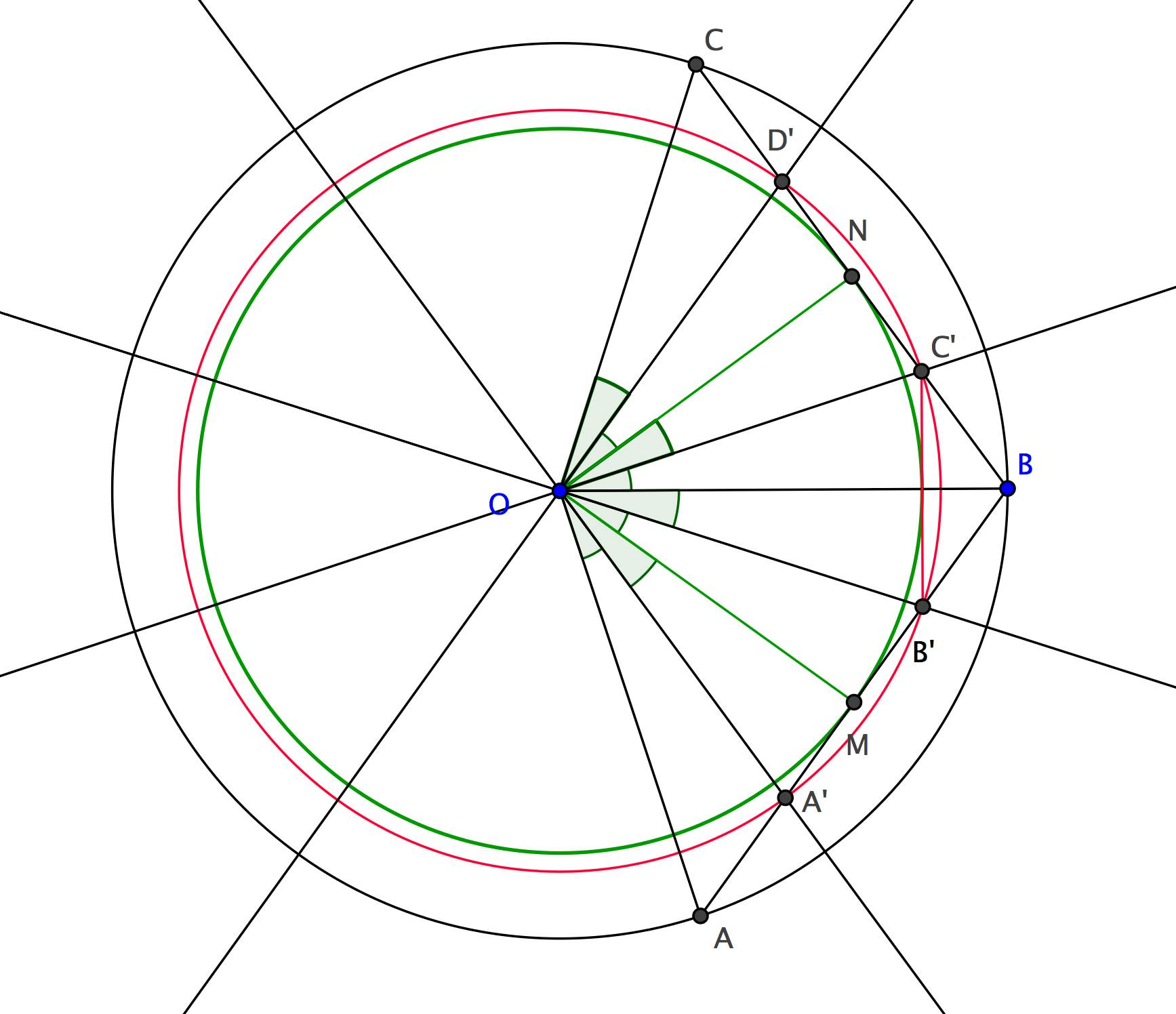
Analyse : Soient A, B et C trois sommets consécutifs du polygone régulier et M et N les milieux de [A B] et [B C]. Comme et ont même cercle inscrit, l'intersection de [A B] et de la bissectrice de doit être un sommet A' de .
Synthèse : On appelle A' (resp. B', C' et D') le point d'intersection de la bissectrice de (resp. , et ) avec [A B] (resp. [C D]). Dans les triangles A'O B' et C'O D', la hauteur est bissectrice donc ces triangles sont isocèles. D'autre part, les triangles rectangles M O B' et N O C' sont isométriques par le deuxième cas en effet en plus des angles droits, leurs angles en O sont égaux à par construction et un de leur côté est l'apothème de . On a donc montré que les longueurs O A', O B', O C' et O D' sont égales. Les points A', B', C' et D' sont donc sur un même cercle de centre O. Or les angles au centre , et valent par construction. Les points sont donc des sommets d'un polygone régulier à 2n côtés. On définit de même les autres sommets de sur chaque côté de .
Construction : On construit le point A', intersection de [A B] et de la bissectrice de . Les autres sommets de sont les intersections des côtés de et du cercle centré en O passant par A'.
Construction à l'aide d'un second polygone
Le polygone est inscrit dans un cercle de centre O, on considère le polygone image de par rotation de centre O et d'angle . Les sommets de et sont ceux d'un polygone régulier à 2n côtés inscrit dans . On peut alors montrer que l'intersection de et est un polygone régulier à 2n côtés portés alternativement par ceux de et ceux de .Démonstration dans le cas n = 5
La méthode décrite ici s'applique à tous les cas et est particulièrement rapide quand n est impair. En effet les sommets de sont dans ce cas les symétriques par rapport à O des sommets de .
Construction d'un décagone régulier dans un pentagone
Soit
A B C D E un pentagone régulier inscrit dans un cercle
 de centre
O.
Soit
AA'BB'CC'DD'EE' le décagone régulier inscrit dans le même cercle (
de centre
O.
Soit
AA'BB'CC'DD'EE' le décagone régulier inscrit dans le même cercle (
 etc...
).
etc...
).

Démonstration :
Soient P, Q, R et S ... comme sur la figure. Par exemple, Q (resp. R) est l'intersection de [A'B'] avec [A B] (respectivement [B C]). On va montrer que ces points sont équidistants de O et que les angles au centre sont égaux.
On rappelle que les droites
(A C'),
(B D'),
(C E'),
(D A') et
(E B') sont axes de symétrie pour les deux pentagones.
La symétrie par rapport à
(B D') fixe
O et
B, échange
A' et
B',
A et
C donc elle échange
Q, intersection de
(A'B') et
(A B), et
R, intersection de
(A'B') avec
(B C) . Il en résulte que
[R Q] rencontre
(O B) en son milieu
N qui est aussi le milieu de
[A'B'] et on a :
OQ=OR.
On montre de même que la symétrie par rapport à
(D A') échange
Q et
P et on obtient que
M est le milieu de
[P Q] et de
[A B]. De plus on a :
O Q=O P.
On en déduit les points
P,
Q,
R sont sur un même cercle de centre
O.
On montre de même de proche en proche que les autres sommets du décagone sont sur le cercle de centre
O et de rayon
O P.
D'autre part les triangles rectangles O P M, O Q M, O Q N et O R N ont un côté de longueur O P et un côte de longueur l'apothème O M des pentagones donc ils sont isométriques par le cas des triangles rectangles. On en déduit l'égalité des angles au centre et . On montre de même que tous les angles au centre de P Q R S T U V W X Y sont égaux.
On a montré que l'intersection de A B C D E et de A'B'C'D'E' est un décagone régulier dont les sommets sont sur les côtés de A B C D E. Ce décagone a même cercle inscrit que les deux pentagones puisque M est le milieu de [P Q] et de [A B].
Polygones et aire du disque
- Longueur d'une courbe
- Longueur d'un cercle
- Encadrement de l'aire d'un disque
- Polygones homothétiques
- Aire d'un disque et Démonstrations approchées de la formule de l'aire d'un disque
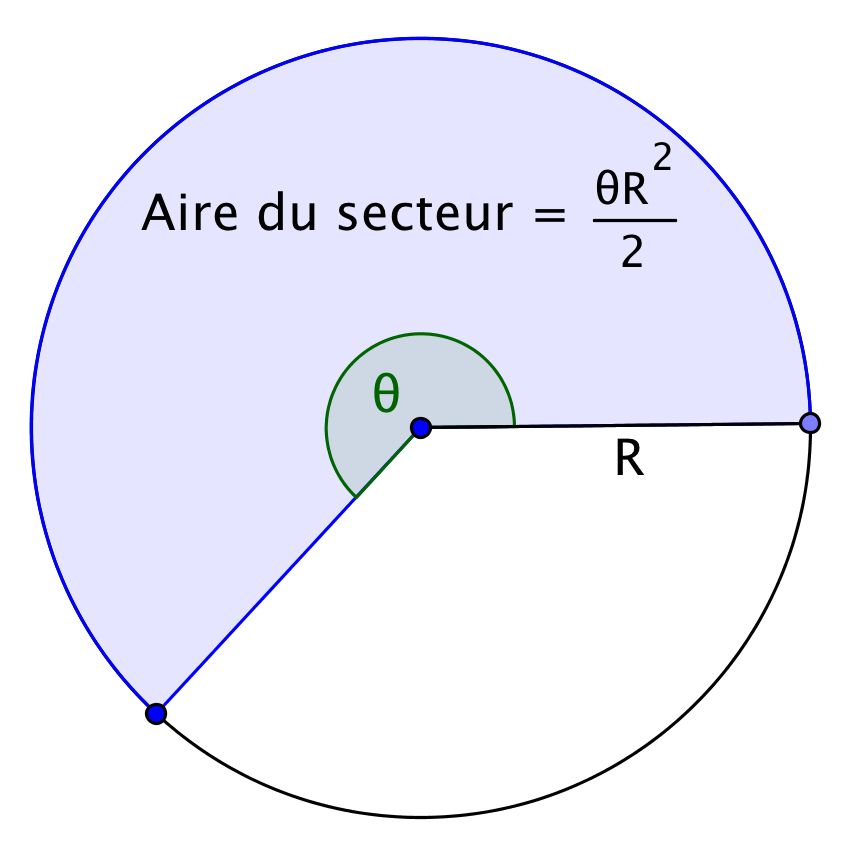
- Aire d'un secteur circulaire
Longueur d'une courbe
Sur la figure, la ligne verte est plus courte que la ligne rouge elle-même plus courte que la courbe noire entre A et G.
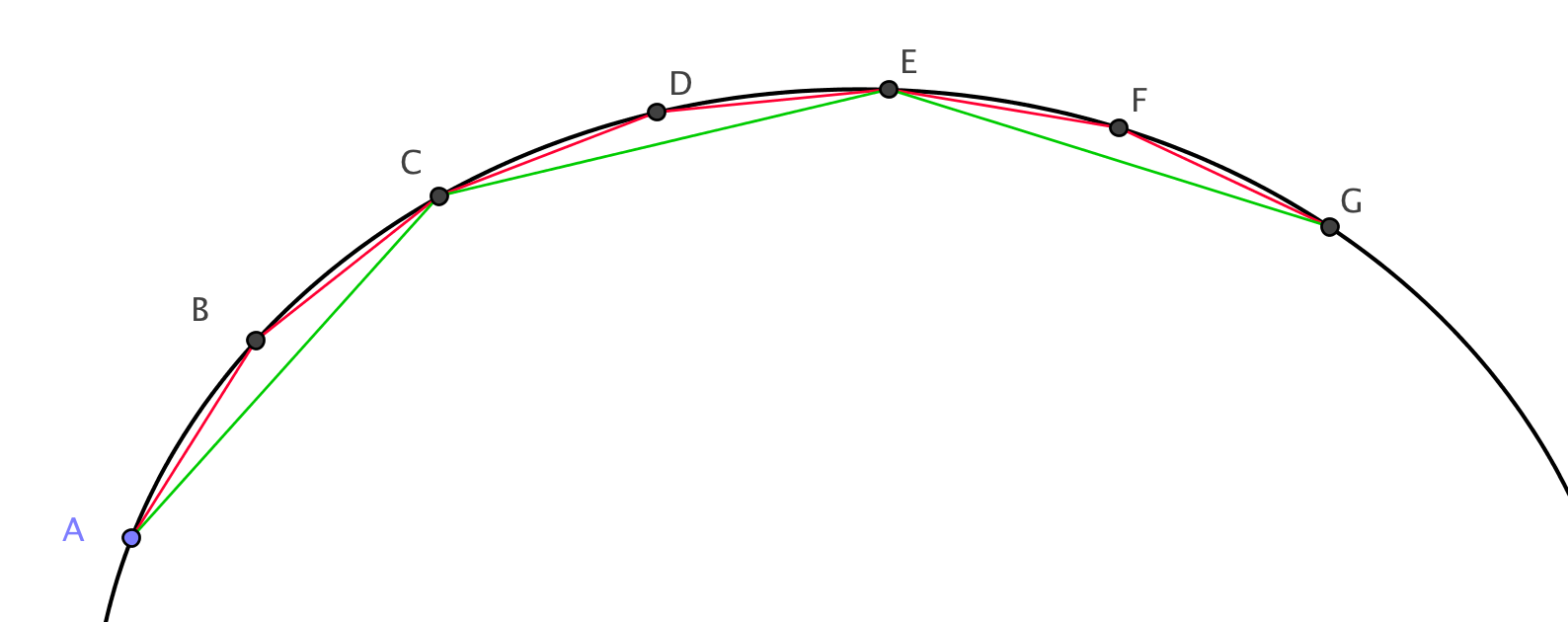
D'autres comparaisons trompeuses :
Comparaison de longueur de courbes
Les courbes bleues, rouges et vertes ont toutes même longueur que le demi-cercle.
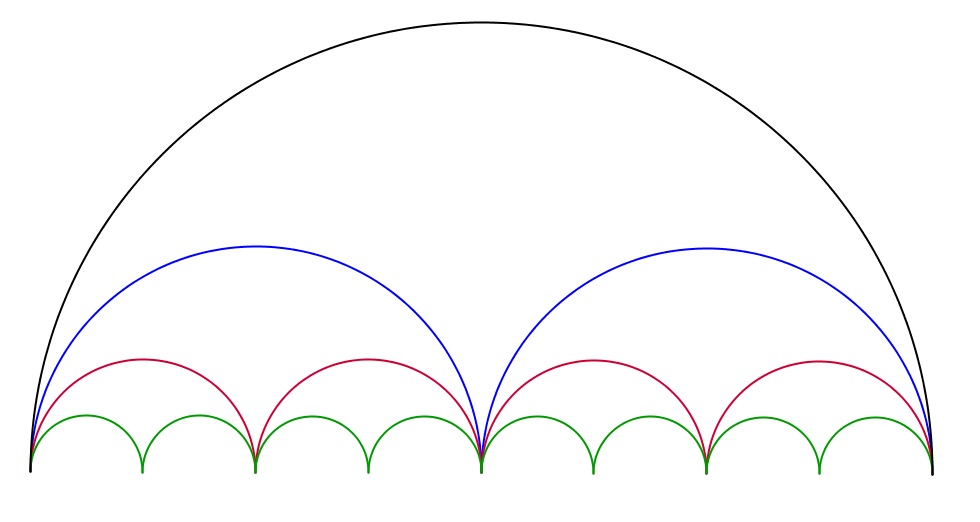
Comparaison de longueur de courbes (suite)
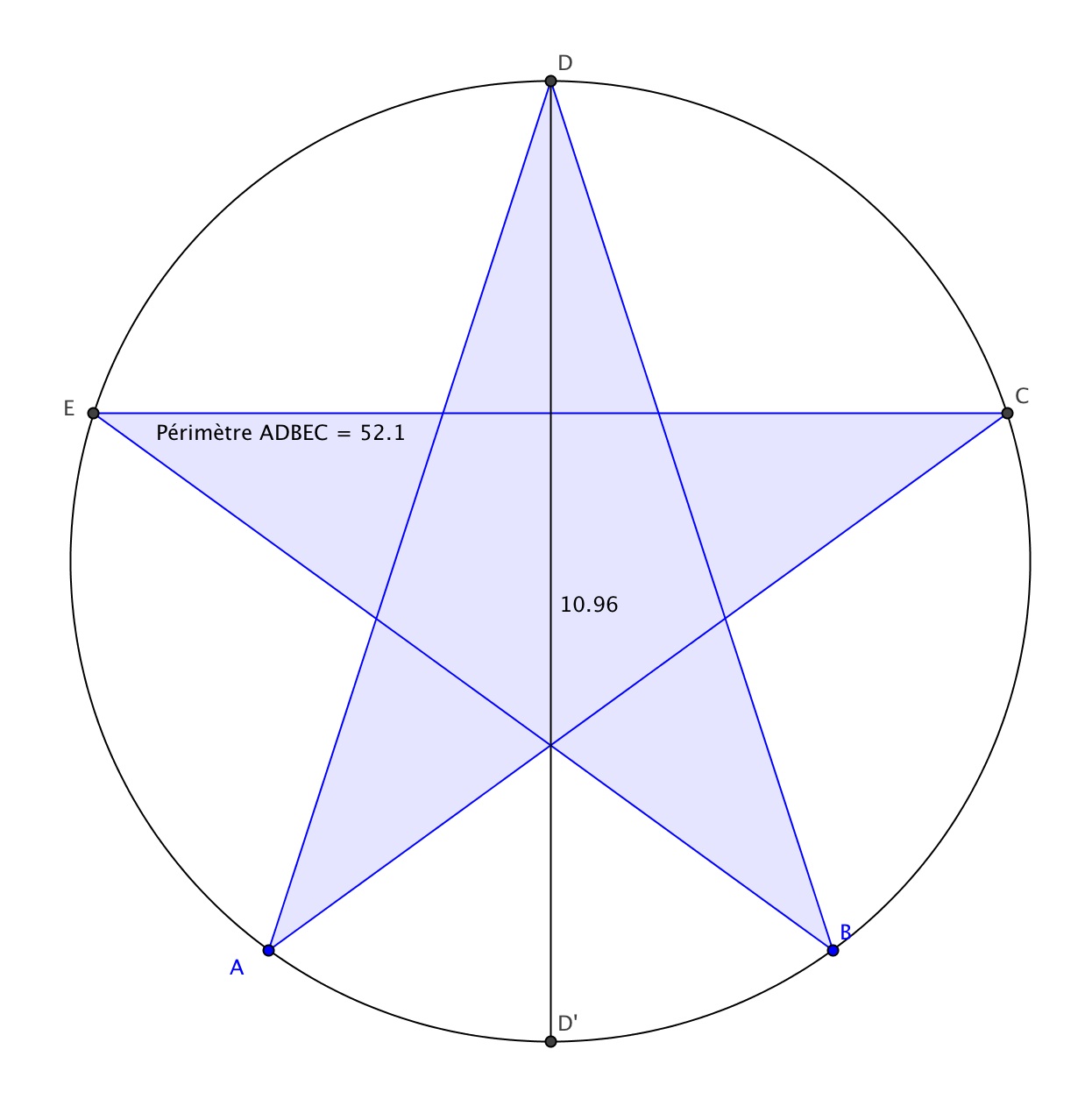
Il est bien sûr possible de tracer dans un disque une courbe de longueur supérieure à la longueur du cercle frontière. Sur cette figure, sont affichés la longueur du diamètre du cercle et le périmètre de l'étoile.
Longueur d'un cercle
 est la longueur d'un demi-cercle de rayon 1.
est la longueur d'un demi-cercle de rayon 1.
Comment calculer une valeur approchée de  ?
?
On en déduit :
- La longueur (ou circonférence) d'un cercle de rayon R est égale à .
- La longueur de l'arc de cercle intercepté sur un cercle de centre
O et de rayon R par un secteur de sommet
O et d'angle
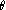 est égale à
est égale à
Valeur approchée de π
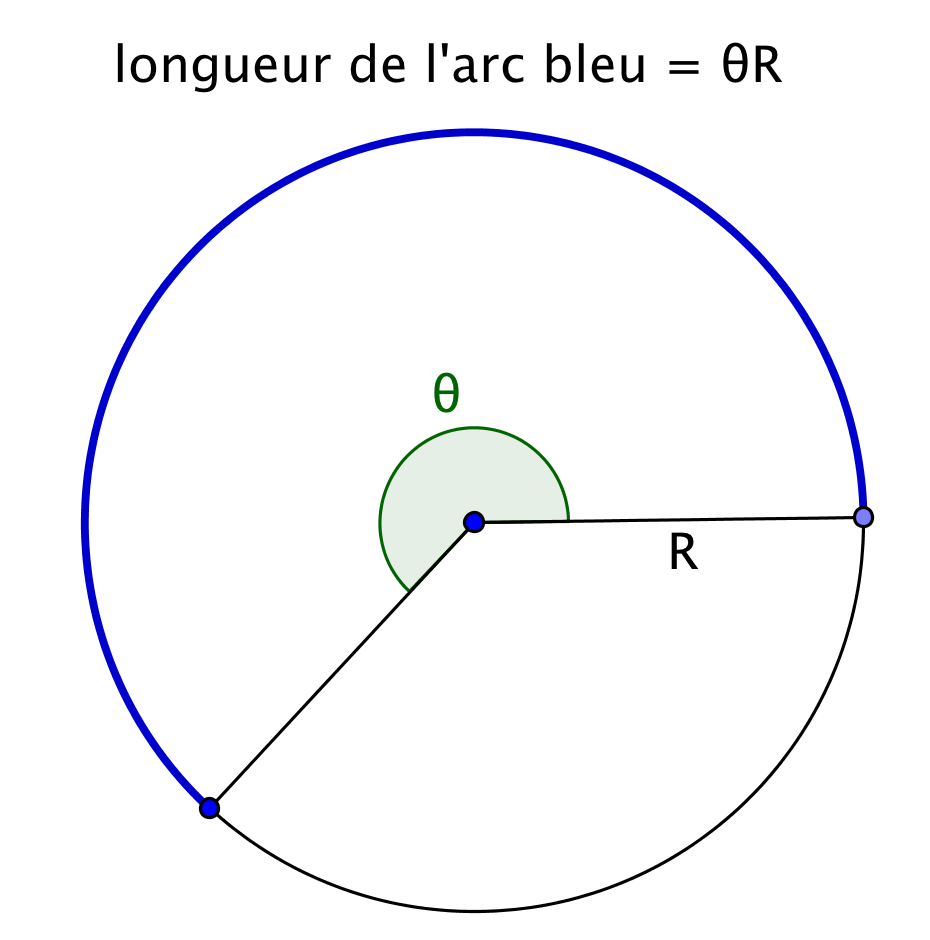
Pour calculer une valeur approchée de , Archimède a utilisé le périmètre
pn d'un polygone convexe régulier à
n côtés inscrit dans un cercle de rayon 1.
En effet par
définition de la longueur d'une courbe
, la limite de
pn quand
n tend vers l'infini est
et pour tout
n,
pn est inférieur à
. [ME VII.4.5]
, Archimède a utilisé le périmètre
pn d'un polygone convexe régulier à
n côtés inscrit dans un cercle de rayon 1.
En effet par
définition de la longueur d'une courbe
, la limite de
pn quand
n tend vers l'infini est
et pour tout
n,
pn est inférieur à
. [ME VII.4.5]
Exemples :
Pour
n = 6 (hexagone bleu), on obtient l'inégalité
.
Pour
n = 12 (dodécagone rouge), l'approximation est bien meilleure :
.
Encadrement de l'aire d'un disque
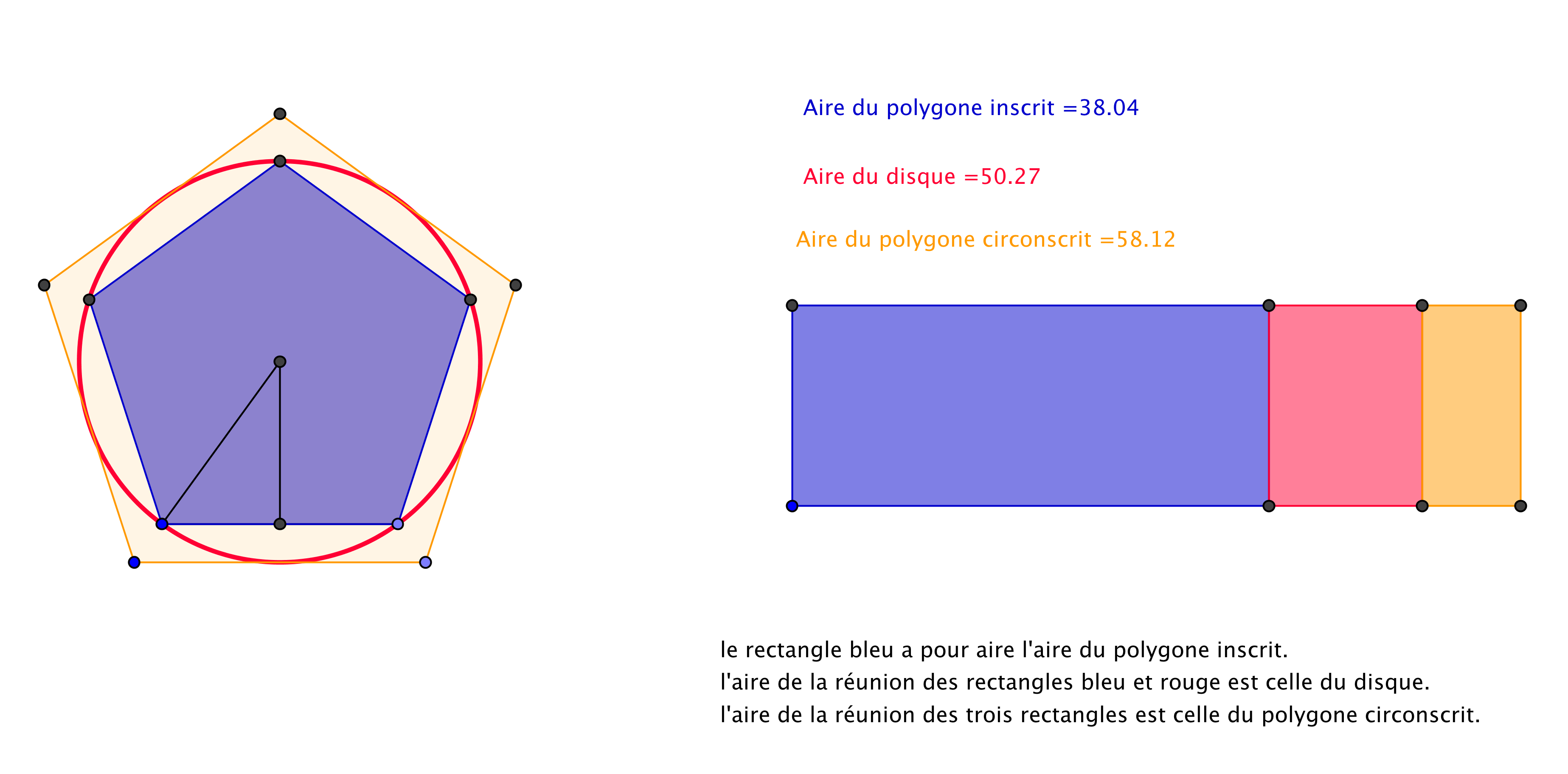
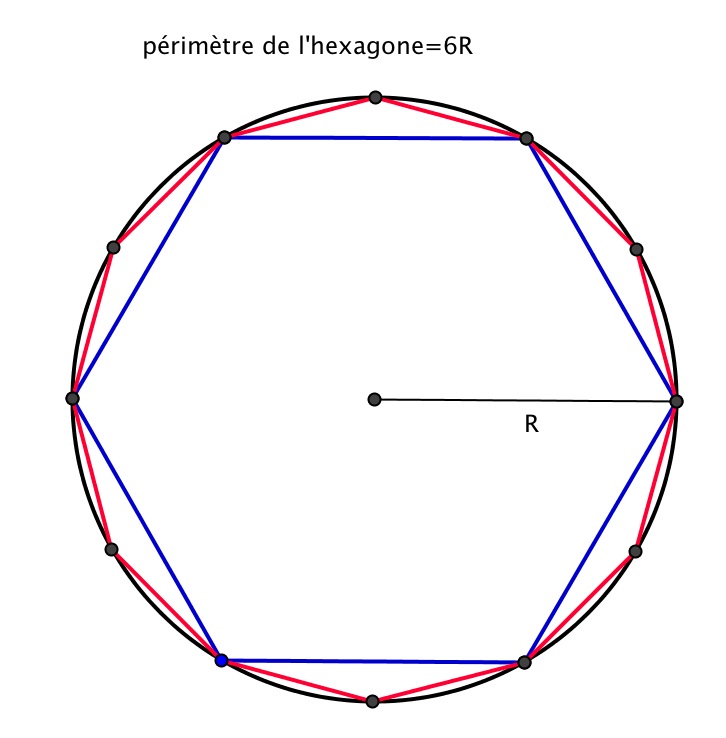
Par additivité de l'aire, l'aire d'un disque
D de frontière
 est supérieure à l'aire d'un polygone
P inscrit dans le cercle
est supérieure à l'aire d'un polygone
P inscrit dans le cercle
 et inférieure à l'aire d'un polygone
Q dont
et inférieure à l'aire d'un polygone
Q dont
 est le cercle inscrit.
est le cercle inscrit.
Dans notre exemple, si le rayon
R de
 est égal à 1, on obtient :
est égal à 1, on obtient :
Aire(Hexagone) < Aire(Disque) < Aire(Carré)
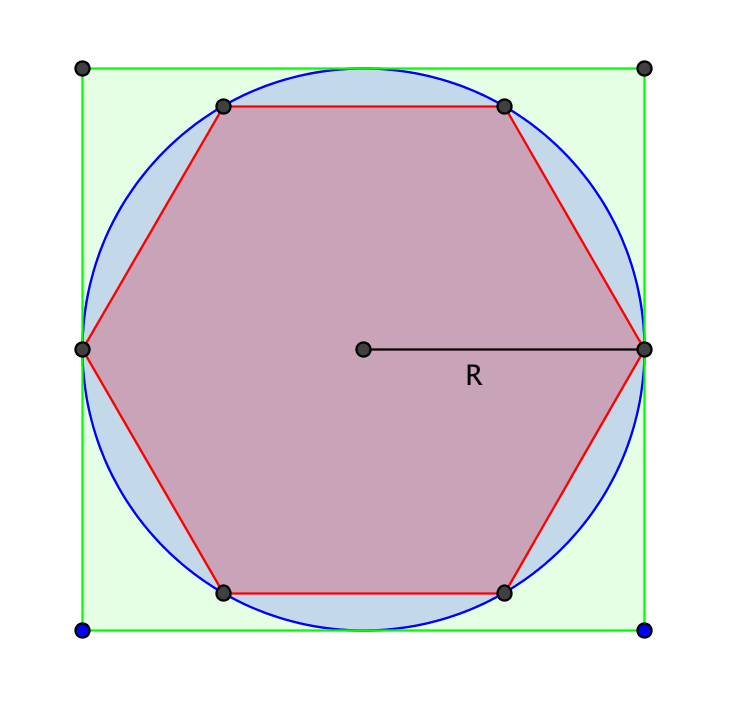
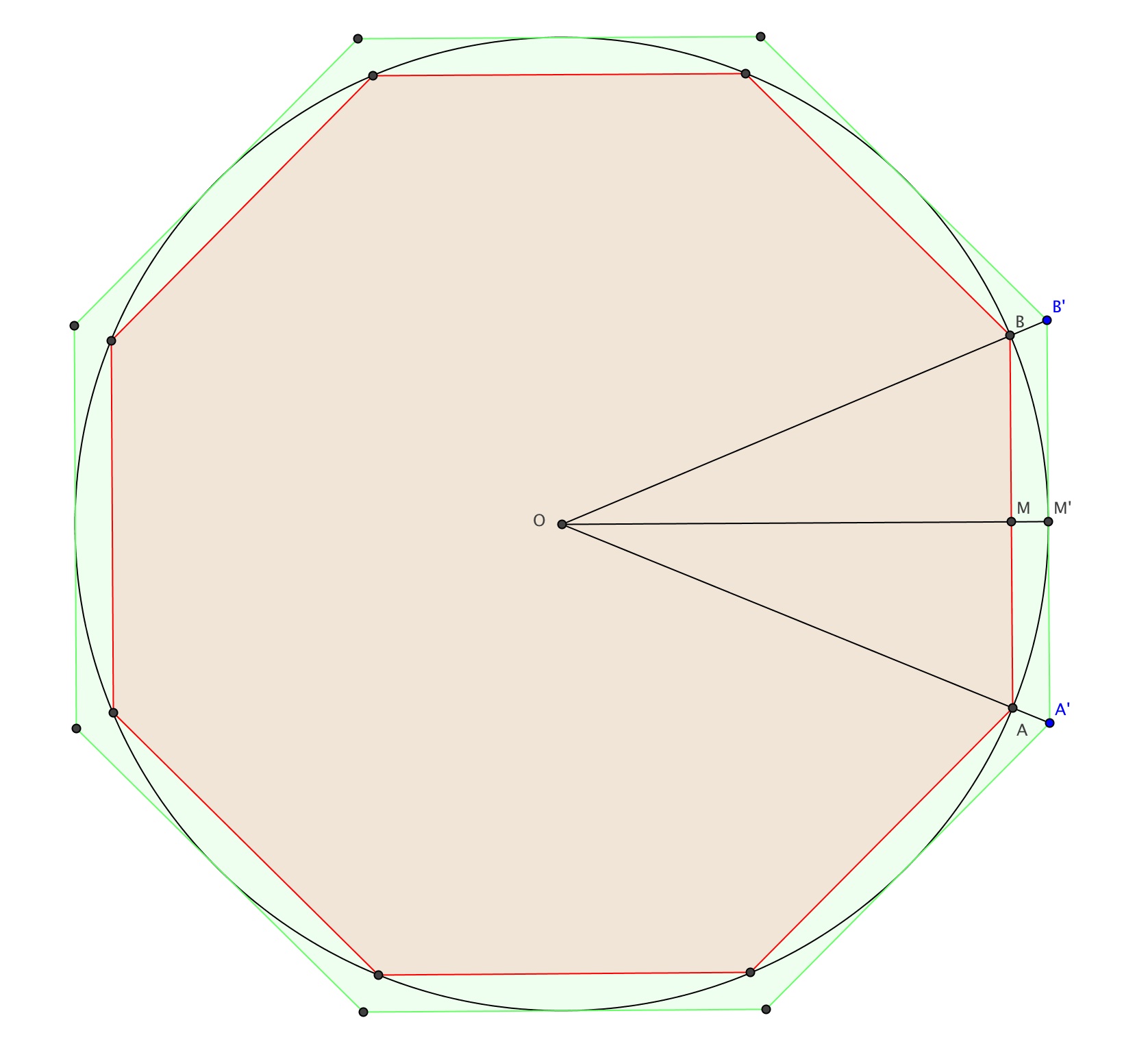
Polygones homothétiques
Soit
Pn un polygone convexe régulier à
n côtés inscrit dans un cercle
 de rayon
R. On note
rn son apothème.
On transforme
Pn par l'homothétie
h de rapport
.
Cette homothétie
h envoie le milieu
M de côté
[AB] sur un point
M' du cercle en effet, de
OM = rn, on déduit
OM' = R.
de rayon
R. On note
rn son apothème.
On transforme
Pn par l'homothétie
h de rapport
.
Cette homothétie
h envoie le milieu
M de côté
[AB] sur un point
M' du cercle en effet, de
OM = rn, on déduit
OM' = R.
L'homothétie
h transforme
Pn en un polygone convexe régulier à
n côtés, appelé
Qn. Comme l'apothème de
Qn est
R = OM', le cercle
 est inscrit dans
Q.
Par homogénéité des aires, on a :
est inscrit dans
Q.
Par homogénéité des aires, on a :
Aire d'un disque
Démonstration : voir [ME page 234, 229].
Version imprimable de la figure de l'aire du disque
Lien vers des Démonstrations approchées de la formule de l'aire d'un disque
Réglez le rayon r et le nombre de côtés n pour que la figure reste lisible.
Version imprimable de la figure de l'aire du disque