Droites et plans (géométrie analytique)
Droites et plans (géométrie analytique)
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Introduction
Avertissement
Dans les parties II et III, on considère l'espace affine muni d'un repère (même si pour les figures, on le prendra orthonormal, il est inutile de lui supposer cette propriété) et on note (x,y,z) les coordonnées d'un point M de dans ce repère. A l'aide de ce repère, on identifie et .
I Droites dans le plan
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Introduction
Dans cette partie, on considère le plan affine muni d'un repère (même si pour les figures, on le prendra orthonormal, il est inutile de lui supposer cette propriété) et on note (x,y) les coordonnées d'un point M de dans ce repère. A l'aide de ce repère, on identifie et .
I-1 Equation cartésienne d'une droite
I-2 Représentation paramétrique d'une droite
Dans les paragraphes suivants, on est amené à résoudre de petits systèmes linéaires. On en profite pour donner quelques éléments pour leur résolution ; ces conseils préparent la méthode de résolution du pivot de Gauss qui sera utilisée dans des cas plus compliqués.I-5 D'une équation cartésienne à une représentation paramétrique
I-6 D'une représentation paramétrique à une équation cartésienne
I-7 Position relative de deux droites
I-1 Equation cartésienne d'une droite
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
I-1-1 Définition : Equation cartésienne d'une droite
I-1-2 Cas particuliers et figure interactive
I-1-3 Détermination d'une équation cartésienne
I-1-1 Définition : Equation cartésienne d'une droite
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
Remarque
Exemple aléatoire
Exercices
Point sur une droite donnée par une équation cartésienne
Droite passant par un point
Sélectionner une équation pour une droite définie par deux points
Remarque
On peut aussi écrire a x + b y - c = 0 l'équation a x + b y = c.
Exemple
I-1-2 Cas particuliers et figure interactive
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
- Cas a=0 : Une droite d'équation b y=c est parallèle à l'axe des abscisses puisque ses points ont tous pour ordonnée
- Cas b=0 : Une droite d'équation a x = c est parallèle à l'axe des ordonnées puisque ses points ont tous pour abscisse
- Cas c=0 : Une droite d'équation a x + b y = 0 passe par l'origine
- Cas b=1 : L'équation réduite d'une droite y = a'x + b' (avec a' et b' deux réels donnés) est un cas particulier d'équation cartésienne.
Figure
Remarque
I-1-3 Détermination d'une équation cartésienne
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Le point M appartient à si et seulement si est colinéaire à . La relation de colinéarité donne une équation cartésienne de : . (Ce résultat est démontré ici .)
Dans le cas d'une droite passant par deux points distincts A et B, on sait que (AB) admet pour vecteur directeur .
Exercices
Sélectionner un vecteur directeur
Equation cartésienne d'une droite passant par deux points avec indication
Equation cartésienne d'une droite passant par deux points sans indication
Equation cartésienne d'une droite donnée par un point et un vecteur directeur
I-2 Représentation paramétrique d'une droite
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
I-2-1 Définition
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
On appelle une représentation paramétrique (de paramètre réel t) de .
Démonstration
Consultez l'exemple à la page suivante.
Exercice
I-2-2 Exemple
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple aléatoire
Le point B de coordonnées ( ; ) est le point de qui correspond à la valeur t= -2 dans cette représentation. Le vecteur est égal à .
Le vecteur est aussi un vecteur directeur de puisqu'il est colinéaire à . Quand on écrit comme la droite passant par B et dirigée par , on obtient la représentation paramétrique :
Dans cette représentation, le point A correspond à la valeur s= -1.
I-3 Direction d'une droite
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
Définition
I-3-1 Direction d'une droite donnée par une représentation paramétrique
I-3-2 Direction d'une droite donnée par une équation cartésienne
I-3-1 Direction d'une droite donnée par une représentation paramétrique
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
Exercice
Représentation paramétrique d'une parallèle
I-3-2 Direction d'une droite donnée par une équation cartésienne
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
Démonstration
Soit un vecteur directeur de . Il s'écrit avec M0 et M1 deux points distincts de ; leurs coordonnées respectives (x0, y0) et (x1,y1) vérifient l'équation a x + b y = c, c'est-à-dire on a : a x0 + b y0 = c et a x1 + b y1 = c. Par différence, on obtient a(x1-x0)+b(y1-y0)=0. Ainsi les composantes du vecteur vérifient l'équation homogène a x + b y = 0. On en déduit que la direction de est contenue dans l'ensemble des solutions de a x + b y = 0. Le vecteur nul est bien sûr solution de a x + b y = 0.
Il reste à montrer que tout vecteur non nul solution de a x + b y = 0 est directeur de . Soit une solution non nulle de a x + b y = 0 et M0 un point de de coordonnés (x0,y0). Soit M1 le point défini par . Les coordonnées de M1 sont . Le point M1 appartient à , en effet on a :
Remarque
Exercices
Equation d'une parallèle à une droite donnée par une équation
Equation d'une parallèle donnée par une représentation paramétrique.
I-4 Systèmes linéaires
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
Exemple
Exemple
Exemple
Remarque
I-5 D'une équation cartésienne à une représentation paramétrique
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Soit une droite d'équation cartésienne a x + b y = c avec . Donner une représentation paramétrique de , c'est résoudre l'équation a x + b y = 0 comme on l'a fait dans un exemple de systèmes linéaires (voir ici ).
Si b est nul, a ne l'est pas. On n'a pas de contrainte sur y à qui on donne la valeur t ; une représentation paramétrique de est donc
Si b n'est pas nul, on pose x=b t (on pourrait aussi poser x=t ou x=25a t, on a le choix) et on calcule y ; après division par b (qui n'est pas nul), on obtient . Une représentation paramétrique de est donc
Remarque
I-6 D'une représentation paramétrique à une équation cartésienne
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
I-6-1 Méthode
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
Démonstration
- Cas : Une équation cartésienne de est x=xA. En effet si la condition x=xA est vérifiée, on peut calculer t puisque, si est nul, ne l'est pas ; on obtient .
- Cas
: Le système
est équivalent au système En effet on a remplacé la ligne L2 par et, pour passer de à , il suffit de remplacer L'2 par . Le système a une solution en t (cette solution est ) si et seulement si x et y vérifientCette équation est donc une équation cartésienne de et la condition de compatibilité du système en t.
Remarque
Exercice
I-6-2 Exemple et figure
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple aléatoire
Figure
I-7 Position relative de deux droites
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Soient et deux droites d'équations cartésiennes respectives a x + b y = c et a'x + b'y = c' (avec et bien sûr). L'intersection de et ou l'ensemble de leurs points communs est l'ensemble des points dont les coordonnées vérifient les deux équations donc c'est l'ensemble des solutions du système de deux équations à deux inconnues x et y.
I-7-2 Droites strictement parallèles
I-7-4 Figure et exercice
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exercice
Position relative de deux droites, système linéaire
Figure à observer dans ses variations :
Sur cette figure, la droite verte D est fixe, elle est dirigée par le vecteur . La droite rouge est la droite passant par M et dirigée par . Le point P est le point d'intersection des deux droites, quand il existe. Faites varier pour tester l'existence de P. Observez les équations des droites.
Faites varier et M pour superposer les deux droites.
I-7-1 Droites sécantes
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple
I-7-2 Droites strictement parallèles
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple
Géométriquement ceci signifie que et sont parallèles (voir la définition ici ). On le constate aussi en remarquant les équations 2x + 4y = 0 et 6x + 12y = 0 de leurs directions sont proportionnelles (voir direction ).
I-7-3 Droites confondues
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple
II Plans dans l'espace
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Introduction
II-1 De la définition géométrique à une représentation paramétrique
II-2 D'une représentation paramétrique à une équation cartésienne
II-3 D'une équation cartésienne à une représentation paramétrique
II-4 Direction d'un plan de l'espace
II-5 Intersection de deux plans dans l'espace
II-1 De la définition géométrique à une représentation paramétrique
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
Si A a pour coordonnées (x0,y0,z0) et (respectivement ) pour composantes (respectivement ). Une représentation paramétrique (de paramètres t et s) de ce plan est :
La représentation paramétrique traduit analytiquement cette équivalence.
Exercice
Point d'un plan donné par une représentation paramétrique
II-2 D'une représentation paramétrique à une équation cartésienne
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple
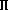 passant par
et dirigé par
et
. Une représentation paramétrique de
passant par
et dirigé par
et
. Une représentation paramétrique de
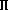 est :
est :
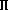 .
.Remplaçons (x,y,z) par les coordonnées (3,1,1) de N dans le système . La première équation donne t=2 et la seconde s=1. Si on s'arrête ici, satisfait d'avoir des valeurs pour t et s, on néglige la troisième équation qui n'admet pas cette solution (2,1), en effet on a . Pour le point N, le système est incompatible, les coordonnées de N ne vérifie pas la condition de compatibilité du système. Il n'existe aucun couple (t,s) tel que . Le point N n'appartient pas à
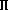 .
.
Exercice
II-3 D'une équation cartésienne à une représentation paramétrique
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Théorème
On dit que a x + b y + c z = d est une équation cartésienne de . Pour tout réel
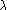 non nul,
est aussi une équation cartésienne de
.
non nul,
est aussi une équation cartésienne de
.
Démonstration
Au moins l'un des coefficients a, b et c n'est pas nul, supposons que a n'est pas nul. Si on pose y = t et z = s de l'équation a x + b y + c z = d, on tire . L'ensemble est donc le plan passant par et dirigé par les vecteurs de composantes et qui ne sont pas colinéaires.
Une représentation paramétrique pour ce plan est
Exemple
Exemple
Exercices
Point d'un plan défini par une équation cartésienne.
Représentation paramétrique d'un plan défini par une équation cartésienne.
II-4 Direction d'un plan de l'espace
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
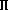 de l'espace.
On appelle direction de
de l'espace.
On appelle direction de
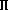 , et on note
, l'ensemble des vecteurs
avec
et
.
, et on note
, l'ensemble des vecteurs
avec
et
.
Proposition
Soit le plan d'équation cartésienne a x + b y +c z = d avec . La direction de est l'ensemble des solutions de l'équation a x + b y +c z = 0. On appelle l'équation a x + b y +c z = 0 l'équation homogène associée à a x + b y +c z = d.
L'affirmation pour résulte des définitions. L'affirmation pour se démontre comme pour la droite ici .
II-5 Intersection de deux plans dans l'espace
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
II-5-3 Figure pour deux plans non parallèles
II-5-4 Intersection de deux plans dans l'espace
II-5-1 Plans parallèles
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
Proposition
Démonstration
Figure
Exercice
II-5-2 Plans non parallèles
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple
Interprétons géométriquement ce résultat : l'intersection de et d'équations respectives x + 2y = 3 et 2x + 4y + z = 8 est l'ensemble des points M de coordonnées (x ,y ,z) vérifiant
Exemple
Interprétons géométriquement ce résultat : l'intersection de et d'équations respectives - 2y + 2z = 4 et x +3z = 5 est l'ensemble des points M de coordonnées (x ,y ,z) vérifiant
Exercice
II-5-3 Figure pour deux plans non parallèles
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Sur la figure suivante qui peut tourner, le plan vert est le plan défini par les points A, B et M1. Le plan rose est le plan passant par A, B et M2. L'intersection des deux plans qui sont en général disjoints est en général la droite (AB). Les plans peuvent-ils être confondus ?
II-5-4 Intersection de deux plans dans l'espace
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
III Droites dans l'espace
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
III-1 Représentation paramétrique
III-2 Système d'équations cartésiennes
III-3 Position relative d'une droite et d'un plan
III-4 Position relative de deux droites
III-1 Représentation paramétrique
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Définition
Un point M (x,y,z) appartient à si et seulement si le système a une solution en t pour (x, y, z).
Exercice
Représentation paramétrique d'une droite donnée géométriquement.
III-2 Système d'équations cartésiennes
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
III-2-1 Conditions de compatibilité de
III-2-1 Conditions de compatibilité de
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Comme n'est pas nul, l'un au moins des réels , et n'est pas nul. Supposons que c'est .
-
[ cas ]
Dans ce cas, les conditions de compatibilité sont y = yA et z = zA et on a : . La droite est intersection de deux plans parallèles aux plans de coordonnées. Un système d'équations cartésiennes de est
-
[ cas et ]
Dans ce cas, une condition de compatibilité est z = zA. L'autre est celle (déjà vue ici ) du systèmesoit . \ Un système d'équations cartésiennes de est alorsLa droite est intersection de deux plans. On calcule .
-
[ cas et ]
L'échelonnement du systèmepermet d'obtenir le système équivalent suivant :Le système a deux conditions de compatibilité qui forment un système d'équations cartésiennes de . Si M appartient à ces deux plans d'équations et , il appartient à en effet on a : pour la valeur .
Proposition
Donner un système d'équations cartésiennes de , c'est considérer comme intersection de deux plans.
III-2-2 Exemple et exercice
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exemple
Exercice
Système d'équations cartésiennes d'une droite
III-2-3 Intersection de plans
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Soit A un point de l'espace et un vecteur non nul et la droite passant par A et dirigée par . Considérons un des vecteurs du repère qui ne soit pas colinéaire à et nommons le plan passant par A et dirigé par et . Le plan contient .
Considérons un des vecteurs du repère qui ne soit pas dans . C'est possible car le repère ne peut pas s'aplatir sur le plan. Nommons le plan passant par A et dirigé par et (qui ne sont pas colinéaires). La droite est contenue dans et qui ne sont pas parallèles donc est l'intersection des plans et .
Exemple
En utilisant la méthode géométrique, on peut choisir et , peut être vue comme l'intersection du plan passant par C et dirigé par et (une équation de ce plan est y - z = -2) et du plan passant par C et dirigé par et (une équation de ce plan est x + 3y = -1).
Remarque
III-3 Position relative d'une droite et d'un plan
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
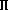 un plan de l'espace
.
Si la direction de
un plan de l'espace
.
Si la direction de
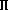 contient un vecteur directeur de
alors on dit que
est parallèle à
contient un vecteur directeur de
alors on dit que
est parallèle à
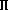 . La droite
peut être contenue dans
. La droite
peut être contenue dans
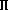 ; sinon on dit qu'elle est strictement parallèle à
; sinon on dit qu'elle est strictement parallèle à
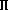 .
Quand
n'est pas parallèle à
.
Quand
n'est pas parallèle à
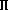 ,
et
,
et
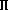 ont un unique point d'intersection.
ont un unique point d'intersection.
Exercices
Intersection d'une droite et d'un plan
Position relative d'une droite et d'un plan
III-4 Position relative de deux droites
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
III-4-3 Exercices dans un cube
III-4-1 Proposition
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Proposition
Si et ont même direction, elles sont strictement parallèles ou confondues.
Si et n'ont pas même direction, deux cas peuvent se présenter :
- elles sont sécantes, c'est-à-dire que leur intersection est réduite à un point.
- elles sont disjointes alors elles sont non coplanaires, c'est-à-dire qu'il existe aucun plan qui les contienne toutes les deux.
Démonstration
Réciproquement, supposons que (respectivement ) est la droite passant par A1 (resp. A2) et dirigée par (resp. ). Si elles sont sécantes en un unique point B, elles sont contenues dans le plan passant par B et dirigé par . Si elles sont parallèles et distinctes, elles sont contenues dans le plan passant par A1 et dirigé par .
Exercices
Position relative de deux droites données par représentation paramétrique.
Position relative de deux droites données par un point et un vecteur directeur
III-4-2 Figure dans un prisme
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Figure
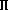 le plan de ce parallélogramme.
le plan de ce parallélogramme.
- Dans le plan
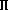 , les droites
(AB) et
(BC) sont sécantes en
B,
, les droites
(AB) et
(BC) sont sécantes en
B,
- Dans le plan
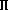 , les droites
(AB) et
(CD) sont parallèles.
, les droites
(AB) et
(CD) sont parallèles.
- La droite
(B'C') est parallèle à
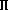 .
.
- La droite
(B'C') est parallèle à
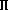 .
.
- La droite
(BB') rencontre
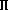 en
B.
en
B.
- Les droites (AB) et (B'C') ne sont pas coplanaires.
III-4-3 Exercices dans un cube
-
I Droites dans le plan
- I-1 Equation cartésienne d'une droite
- I-2 Représentation paramétrique d'une droite
- I-3 Direction d'une droite
- I-4 Systèmes linéaires
- I-5 D'une équation cartésienne à une représentation paramétrique
- I-6 D'une représentation paramétrique à une équation cartésienne
- I-7 Position relative de deux droites
- II Plans dans l'espace
- III Droites dans l'espace
Exercices
Droite et plan dans un cube (facile)
Droite et plan dans un cube
Position relative de deux droites dans un cube (facile)
Position relative de deux droites dans un cube