Raisonnements
Objectifs
Ce module est consacré au langage et au raisonnement en mathématiques ainsi qu'à la théorie des ensembles. Son objectif essentiel est que de donner tout son sens à une proposition écrite avec des symboles mathématiques et d'apprendre à les utiliser avec précision (et non comme des abréviations).Documents
- F. Liret et D. Martinais, Mathématiques pour le DEUG, Algèbre 1ère Année (Dunod), chapitre 1
- A. Auzimour et F. Petit, Travaux dirigés d'algèbre (Vuibert)
- A. Denmat et F. Héaulme, Algèbre générale (Dunod), td 1
Guide
Outils de base
- Assertions
- Connecteurs
- Quantificateurs
- Implication
- Condition nécessaire, condition suffisante
- Contraposée
Assertions
- Il est jaune est une assertion incomplète, je ne pourrai jamais
décider si elle est fausse ou vraie.
Une assertion est une affirmation à laquelle on peut attribuer la valeur vraie ou fausse.
- Le stylo de Marianne est noir est par contre une assertion au moins s'il n'y a qu'une seule Marianne et qu'elle n'a qu'un seul stylo.
- x est plus grand que y est une assertion incomplète.
- Soit x un homme, il est brun ou Tous les hommes sont bruns sont des assertions.
- est une assertion incomplète.
- Tous les entiers naturels vérifient est une assertion (fausse mais une assertion quand même !)
- n'est pas une assertion complète. En tout cas, elle dépend du contexte dans lequel on se trouve.
Connecteurs
Les connecteurs et et ou sont liés à l'intersection et à la réunion des ensembles et la négation est liée au complémentaire d'un ensemble Si \calP est une assertion, non \calP est l'assertion qui est vraie si \calP est fausse et fausse si \calP est vraie. Remarquez que cette définition contient la règle du tiers exclu : Une assertion \calP est vraie ou fausse.
Ce sont des moyens de produire une nouvelle
assertion à partir de deux autres : par exemple
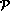 et
et 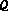 <----->
est l'ensemble des éléments qui appartiennent
à
X et à
Y.
<----->
est l'ensemble des éléments qui appartiennent
à
X et à
Y.
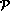 ou
ou 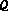 <----->
est l'ensemble des éléments qui appartiennent
à
X ou à
Y.
<----->
est l'ensemble des éléments qui appartiennent
à
X ou à
Y.
non 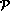 <----->
est l'ensemble des éléments qui
n' appartiennent pas à
X.
<----->
est l'ensemble des éléments qui
n' appartiennent pas à
X.
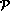 <----->
est l'ensemble des éléments qui
n' appartiennent pas à
X.
<----->
est l'ensemble des éléments qui
n' appartiennent pas à
X.
Quantificateurs
Les quantificateurs sont- quelquesoit noté
- il existe noté .
Exercice :
Le langage courant utilise tout le temps des
quantificateurs. Essayez
de les détecter et donnez la négation des assertions qui les
utilisent dans l'exercice
Négation
.
Exercice : Écrire à l'aide de quantificateurs les
phrases suivantes
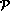 : tous les guichets sont fermés certains jours
: tous les guichets sont fermés certains jours
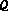 : certains jours tous les guichets sont fermés
: certains jours tous les guichets sont fermés
Ecrire leur négation en langage courant et avec des quantificateurs.
Solution
(P) tous les guichets sont fermés certains jours :
(Q) certains jours tous les guichets sont fermés :
(non P ): certains guichets sont ouverts tous les jours :
(non Q ): tous les jours, il y a un guichet d'ouvert :
Vous pouvez remarquer que c'est plutôt plus simple mathématiquement : on remplace par , on remplace par et on remplace g est fermé par sa négation qui est ici g est ouvert
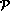 : tous les guichets sont fermés certains jours
: tous les guichets sont fermés certains jours
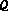 : certains jours tous les guichets sont fermés
: certains jours tous les guichets sont fermés
Ecrire leur négation en langage courant et avec des quantificateurs.
Solution
(P) tous les guichets sont fermés certains jours :
(Q) certains jours tous les guichets sont fermés :
(non P ): certains guichets sont ouverts tous les jours :
(non Q ): tous les jours, il y a un guichet d'ouvert :
Vous pouvez remarquer que c'est plutôt plus simple mathématiquement : on remplace par , on remplace par et on remplace g est fermé par sa négation qui est ici g est ouvert
Exercice :
On note
P l'ensemble des portes d'un lycée qui
sont munies d'une
serrure et
C l'ensemble des clés que possède le concierge de ce
lycée. Quel est le
sens en français courant et concret des
assertions mathématiques suivantes :
Implication
Il est important de bien connaître le sens du symbole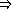 , c'est-à-dire de
l'
implication
, c'est-à-dire de
l'
implication
Si P et Q sont deux propriétés
(assertions), P
Q (qui se lit
P implique Q )
est la propriété
non P ou Q.
En particulier,
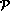
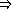
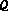 peut être vraie ou faux, il s'agit
d'une assertion.
Cependant, par abus de langage, il arrive à tout le monde de dire
"On a
peut être vraie ou faux, il s'agit
d'une assertion.
Cependant, par abus de langage, il arrive à tout le monde de dire
"On a 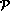
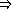
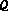 " ou pire, " si
" ou pire, " si 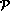
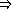
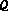 , alors ...."
, alors ...."
Condition nécessaire, condition suffisante
Quelques rappels sur conditions nécessaire, condition suffisante :
Si 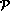 et
et 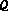 sont des
propriétés (assertions),
sont des
propriétés (assertions),
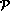 et
et 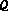 sont des
propriétés (assertions),
sont des
propriétés (assertions),
-
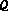 est une condition nécessaire de
est une condition nécessaire de 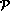 si
si
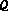 est vraie lorsque
est vraie lorsque 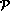 est vraie
est vraie -
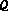 est une condition suffisante de
est une condition suffisante de 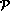 si
si 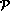 est vraie lorsque
est vraie lorsque 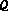 est vraie
est vraie
Dans le langage courant, condition nécessaire, condition suffisante, condition nécessaire et suffisante peuvent se dire d'autres manières en utilisant les mots si , seulement si...
Exercice
sur la
notion de condition nécessaire et condition suffisante
.
Contraposée
Contraposée
La contraposée de l'implication P Q est l'implication non Q non P . C'est une assertion équivalente à l'implication. Pour démontrer qu'une implication est vraie, il suffit de démontrer que sa contraposée implication l'est. Il arrive souvent que la propriété contraposée soit plus "évidente'' à l'intuition que la propriété elle même. Par exemple : Pour montrer que l'implicationL'étude de la contraposée peut aussi éclairer l'affirmation suivante:
si
P est
fausse, alors
P
est vraie.
En effet on admet plus
facilement que si P est fausse, c'est-à-dire si non P est vraie,
la contraposée non Q
non P
est vraie,
puisque non P est vraie.
Une implication et sa contraposée ont donc même valeur de vérité.
Contraposée et réciproque
Il ne faut pas confondre la contraposée d'une implication avec l' implication réciproque : La réciproque de l'implication est l'implication (il s'agit donc d'une autre assertion)
Donnons un exemple en langage courant :
S'il pleut, le sol est mouillé
a pour contraposée :
si le sol
n'est pas mouillé, il ne pleut pas
énoncé plus couramment le sol est
sec, donc il ne pleut pas.
Ces deux implications sont vraies et équivalentes. La réciproque est :
si le sol est mouillé, il pleut.
Cette implication est fausse, le sol peut être mouillé par le passage du camion municipal de nettoyage ou bien par de la neige qui a fondu.
Exercice sur les
contraposées et réciproques
dans le langage courant.
Attention quand même aux pièges de la vie courante !
Exercice sur les
contraposées et réciproques
en mathématiques.
Contraposée et réciproque : pièges de la vie courante
Et en fait dans la vie courante de même que ce qui n'est pas dit est souvent sous-entendu, on confond très souvent contraposée et réciproque : par exemple, si on vous ditsi tu es sage ce matin, tu auras du chocolat cet après-midi
la contraposée est
Si tu n'as pas de chocolat cet après-midi, tu n'as pas été sage ce matin
et la réciproqueSi tu as du chocolat cet après-midi, tu as été sage ce matin.
Enfin, la contraposée de la réciproque est
Si tu n'est pas sage ce matin, tu n'auras pas de chocolat cet après-midi.
Ce qui n'est pas équivalent à la première phrase. Mais c'est en général cette dernière affirmation qui est dans la tête de celui qui prononce la première (en appliquant des principes d'éducation positive !)
Raisonnements
- Règles de raisonnement
- Principe de récurrence
- Raisonnement par l'absurde
- Raisonnement par disjonction des cas
- Un scénario de Lewis Carrol
- Un problème
Règles de raisonnement
Il y a trois règles (principes) suivants qui s'appliquent tout le temps :- si P est vraie et P
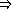 Q vraie,
alors l'assertion Q est vraie.
Q vraie,
alors l'assertion Q est vraie.
Cette règle est en fait une définition de ce que signifie qu'une implication est vraie. On l'emploie tout le temps sans même s'en rendre compte.
ExempleConsidérons la fonction f définie sur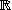 par
f(x)= x3+1.
L'implication
f est dérivable surest vraie. Comme f est dérivable sur
par
f(x)= x3+1.
L'implication
f est dérivable surest vraie. Comme f est dérivable sur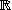
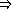 f est continue sur
f est continue sur
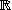
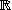 ,
f est continue sur
,
f est continue sur 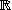 .
.
- Si P est vraie, si P
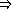 Q vraie, si Q
Q vraie, si Q
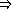 R est vraie, alors R est vraie.
R est vraie, alors R est vraie.
C'est ce qu'on appelle un syllogisme. -
Raisonnement par dichotomie ou séparation des cas : on essaye un cas puis l'autre.
Le raisonnement par séparation des cas consiste à énumérer les cas
possibles.
Exemple
Exercice : Trois frères Alfred, Bernard et Claude ont des crayons de couleur différente bleu, rouge et vert. De plus, les assertions suivantes sont vraies :
- Si le crayon d'Alfred est vert, alors le crayon de Bernard est bleu ;
- Si le crayon d'Alfred est bleu, alors le crayon de Bernard est rouge ;
- Si le crayon de Bernard n'est pas vert, alors le crayon de Claude est bleu
- Si le crayon de Claude est rouge, alors le crayon d'Alfred est bleu.
Que peut-on conclure sur la couleur respective des crayons d'Alfred, Bernard et Claude? Y a-t-il plusieurs possibilités ?
Aide : Faites l'hypothèse que le crayon d'Alfred est vert et voyez ce qu'on peut en déduire. Si vous en déduisez que le crayon d'un autre est à la fois de deux couleurs différentes ou que deux des frères ont des crayons de même couleur, c'est que cela n'est pas possible. Faites alors une autre hypothèse.Solution : Le crayon d'Alfred est rouge, celui de Bernard est vert et celui de Claude est bleu.
Les autres types de raisonnement sont
Raisonnement par l'absurde
Le raisonnement par l'absurde consiste à supposer le contraire de ce que l'on veut démontrer, puis par des déductions logiques (utilisant l'hypothèse) à aboutir à une absurdité. Exemple :
On veut démontrer que
n'est pas un rationnel. Pour cela,
on va supposer que
est rationnel. On écrit
avec
p
et
q des entiers premiers entre eux. On va ensuite déduire de
l'équation
q2 = 2p2 que
p et
q sont pairs.
Ce qui est en contradiction avec le choix de
p et
q qu'on a fait
(ils sont premiers entre eux).
Parfois on traite de raisonnement , par l'absurde, un simple raisonnement utilisant la contraposée. Par exemple,
- on veut démontrer que
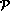
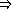
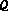 est vraie,
est vraie,
- on suppose non
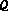 ,
, - on finit par démontrer non
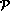 et on se dit en contradiction avec
et on se dit en contradiction avec 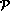 mais
mais 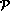 ne nous a pas
servi. Il n'y a donc pas de contradiction mais une simple contraposée.
ne nous a pas
servi. Il n'y a donc pas de contradiction mais une simple contraposée.
Raisonnement par disjonction des cas
Pour montrer une propriété par disjonction des cas, on la prouve dans un nombre fini de cas, ces cas couvrant tous les cas possibles.
Exercice :
Montrer qu'il existe deux irrationnels
a et
b tels que
ab
soit rationnel.
Aide
Aide
Raisonner selon que
est
rationnel ou non.
Solution
Rappelons que
est irrationnel.
Soit
est rationnel, soit il ne l'est pas et alors il est irrationnel.
- Si est rationnel, on a fini. Les nombres a= et b= conviennent.
- Sinon les nombres et sont irrationnels et ab vaut 2.
Un scénario de Lewis Carrol
Considérons le problème suivant sachant que chacune des assertions suivantes est vraie :- Ou le malfaiteur est venu en voiture, ou le témoin s'est trompé ;
- Si le malfaiteur a un complice, alors il est venu en voiture ;
- Le malfaiteur n'avait pas de complice et n'avait pas la clé ou bien le malfaiteur avait un complice et avait la clé ;
- Le malfaiteur avait la clé.
Que peut-on en conclure ? Si on remplace la dernière par le malfaiteur n'avait pas la clé, peut-on conclure ?
Un problème
Exercice :
Trois frères Alfred, Bernard et Claude ont des crayons de couleur différente
bleu, rouge et vert.
De plus, les assertions suivantes sont vraies :
Que peut-on conclure sur la couleur respective des crayons d'Alfred, Bernard et Claude? Y a-t-il plusieurs possibilités ?
- Si le crayon d'Alfred est vert, alors le crayon de Bernard est bleu ;
- Si le crayon d'Alfred est bleu, alors le crayon de Bernard est rouge ;
- Si le crayon de Bernard n'est pas vert, alors le crayon de Claude est bleu
- Si le crayon de Claude est rouge, alors le crayon d'Alfred est bleu.
Que peut-on conclure sur la couleur respective des crayons d'Alfred, Bernard et Claude? Y a-t-il plusieurs possibilités ?
Aide : Faites l'hypothèse que le crayon d'Alfred est vert et voyez ce qu'on peut en déduire. Si vous en déduisez que le crayon d'un autre est à la fois de deux couleurs différentes ou que deux des frères ont des crayons de même couleur, c'est que cela n'est pas possible. Faites alors une autre hypothèse.
Solution : Le crayon d'Alfred est rouge, celui de Bernard est vert et celui de Claude est bleu.
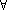 p
p 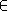 P
P 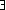 c
c