Dans tous les exercices, la variable est de manière aléatoire x ou t.
Les exercices sont regroupés en deux séries.
Les exercices notés # ne comportent que des équations linéaires à coefficients constants (de la forme ay' + by = ...)
Les autres portent sur des équations de la forme a(t) y' + b(t) y = ... où a(t) et b(t) peuvent être variables ou constantes.
Plusieurs paramétrages sont disponibles en bas de cette page.
Les exercices sont numérotés dans un ordre pouvant correspondre à une progression pédagogique.
L'équation homogène associée à
est :
.
est une solution particulière de
.
L'équation homogène associée à
est :
.
Les solutions de l'équation sont les fonctions définies par
Les solutions de l'équation sont les fonctions définies par
Ecrire l'équation homogène associée à :
.
Une solution particulière de l'équation est
.
L'équation homogène associée à est : .
Les solutions de sont (utiliser la constante k) :
Une solution de l'équation est
.
Les solutions de l'équation sont :
Les solutions de l'équation sont : . Les solutions de l'équation sont : .
Parmi celles-ci, celle qui vérifie est définie par :
Déterminer la solution particulière de cette équation différentielle qui vérifie .
On notera exp(..) ou e^.. la fonction exponentielle.
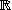 l'équation différentielle :
l'équation différentielle : On utilisera pour désigner une constante réelle, et on notera exp(..) ou e^.. la fonction exponentielle.
ATTENTION : Il faut taper * ou un espace entre et . Par exemple, pour écrire , taper k*e^(3t) ou k e^(3t), MAIS PAS ke^(3t) !
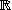 l'équation différentielle (où
désigne une fonction de la variable
):
l'équation différentielle (où
désigne une fonction de la variable
): par (et par sa dérivée) dans et je trouverai
par (et par sa dérivée) dans et je trouverai une expression que j'identifierai ensuite avec
qui donne les solutions de l'équation différentielle où est une constante.
qui donne les solutions de l'équation différentielle , car la méthode précédente ne peut pas s'appliquer.
à la solution générale de l'équation homogène trouvée à la question
par dans la solution générale trouvée à la question ; j'écris que le résultat doit être égal à , je trouverai alors la valeur de et je pourrai répondre à la question.
Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.