Inégalités

Objectifs

Majorer, minorer, encadrer, voici les techniques de base de l'analyse et ce module a pour but de vous entraîner à ces techniques. Il propose aussi une première approche de la définition de la limite.

Guide

Inéquations

Encadrements

Cours : La manipulation des inéqualités est l'occasion de nombreuses erreurs. Ces manipulations s'appuient sur les propriétés de l'ordre de RR .

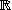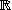Exercices : Ces trois exercices proposent d'encadrer des expressions en x et y connaissant un encadrement des nombres réels x et y.
  1. Encadrement 1
  2. Encadrement 2
  3. Zone d'inégalité

Inéquations : Exercices

Exercice : Sans étude de fonctions mais en utilisant les propriétés de l'ordre de RR, résoudre les inéquations suivantes :

Inéquations : Exercices

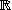Exercice : Résoudre les inéquations :

La racine carrée est-elle définie ?

Solution
  2. .

Exercices de déduction d'inégalités simples

Les exercices qui suivent demandent de montrer des choses simples mais obligent à décomposer en étapes et à réfléchir à chaque instant aux méthodes que l'on utilise et qui doivent ensuite être utilisées "sans réfléchir".
Exercices de déduction (I):

Exercices de déduction (II) : Un pot pourri d'inégalités à résoudre

Exercices de déduction (III) : Borner une fraction

Implication entre inégalités

Quel est le problème ?

Jusqu'à maintenant, vous avez dû résoudre des inéquations, c'est-à- dire chercher tous les x vérifiant une inégalité par exemple : . L'ensemble des solutions est .
Dorénavant, vous allez devoir vérifier qu'une condition sur x est suffisante pour obtenir un certain encadrement d'une fonction, par exemple : L'implication suivante est-elle vraie ?

La condition signifie que x est compris entre 1,5 et 2,5 et implique que est majoré par 4,5, on peut donc écrire.


Quelles sont les méthodes ?

Considérons une fonction numérique f d'une variable x, par exemple

Que peut-on dire des variations de f si x varie dans un intervalle donné I par exemple [1;3] ? On peut évidemment faire une étude complète de la fonction mais souvent une estimation suffit.

Dans notre exemple, f se présente comme une fraction : pour majorer f, nous allons
En conclusion, sur [1;3], on peut dire que la fonction est majorée par 24 et même par 6 si on a été plus courageux.

Exercices

Exercice : Démontrer les implications suivantes :

  1. Solution
    Par hypothèse le réel x est dans l'intervalle [0;2], l'inégalité triangulaire nous permet de majorer le numérateur :

    D'autre part le dénominateur vaut 6- x2 dans l'intervalle considéré donc est minoré par 2.


  2. Solution
    Quand x est positif, exp (-x) est positif et majoré par 1. Quand x est supérieur à 16 alors x6-20x2 est strictement positif et minoré par x6. On obtient donc


  3. Solution
    Par hypothèse, x-2 est compris entre -1 et 1 donc est positif et minoré par (la fonction cosinus est paire de plus elle est décroissante entre 0 et 1) alors que x est minoré par 1. On obtient donc

Approche de la limite

Approche de la définition de la limite

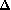Question : Dans quel intervalle autour de a puis-je remplacer f(x) par f(a) sans commettre une erreur supérieure à epsilon ? Par exemple, dans quel voisinage de , est-on sûr de pouvoir remplacer par 2 en commettant une erreur Delta inférieure à ?

Prenons et transformons la différence en valeur absolue de f(x) et de :

Maintenant nous allons majorer par une constante sur un intervalle plus petit contenu dans .

Calcul de l'erreur

D'une part est minoré par 1, d'autre part si x est supérieur à alors est inférieur à 4, donc pour tout x supérieur à ,

est majoré par .


Si x vérifie , x vérifie aussi , La majoration est donc valide et nous avons montré l'implication suivante :


En résumé, si on choisit x entre et , on peut dire que vaut 2 à 10-3 près ou que l'erreur est au plus de 10-3.
Le travail central ici est le travail de majoration, en effet ensuite la détermination de l'intervalle est immédiate. Nous pouvons utiliser ce travail de majoration pour affirmer :

Comme notre majoration n'est valide que pour x supérieur à , condition qui est vérifiée si x appartient à l'intervalle ; on impose la condition . Pour que l'implication soit vraie, il suffit donc de prendre .
Interprétation

Interprétation

L'énoncé mathématique obtenu

signifie que

tend vers 2 quand x tend vers .

Exercices

Exercice : Aide visuelle : epsilon étant donné, trouver alpha en étant aidé visuellement.

Exercice : Donner une majoration raisonnable de de la forme où n est un entier et C un réel positif (on pourra si nécessaire imposer une condition à ) pour :
  1. Solution

    Si la condition est vérifiée, on peut donc écrire :

  2. Solution

    Si x est compris entre 1/2 et 3/2, (on est alors sûr que la fonction est définie) , On minore par (faire un dessin sur la droite réelle en plaçant , 1, et 2) et on majore par . On peut donc écrire que

    si x est compris entre 1/2 et 3/2 ,

  3. Solution

    La fonction est définie seulement si x n'est pas nul, nous allons donc prendre x compris entre et , alors

    est majoré par 4(x-1)2

Exercice : Soit epsilon un réel strictement positif. Dans chacun des cas traités au-dessus, proposer une valeur de alpha dépendant de epsilon telle que l'implication suivante soit vraie :


Solution

Rightarrow

Une infinité de choix de alpha sont possibles, le choix dépend de la majoration qu'on a réussi à faire. Les majorations proposées permettent d'affirmer que les valeurs de alpha suivantes conviennent ainsi que toute valeur inférieure.
  1. . On doit choisir alpha inférieur à 1 car la majoration n'est démontrée que pour .

    ) Rightarrow

  2. .

    Rightarrow

  3. .



document donnant une introduction à la notion de limite.
: limite,inegalite,epsilon,inequation, interactive mathematics, interactive math, server side interactivity

The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.