Vecteurs du plan

Vecteurs du plan


Introduction

Ce document est un résumé (niveau lycée) sur la notion de vecteurs en géométrie élémentaire. Il est destiné à servir d'aide à des exercices de révision sur cette notion.

Avertissement
Ce document est écrit à l'intention d'étudiants entrant dans l'enseignement supérieur. Son contenu est utile pour aborder le cours de physique. Il est aussi pensé comme rappel avant le cours d'algèbre linéaire. C'est pourquoi, on a choisi de distinguer, au moins au départ, les vecteurs géométriques, ceux qu'on dessine précisément dans le plan affine, et les vecteurs abstraits qui sont les classes d'équivalence de vecteurs géométriques. En algèbre linéaire, un vecteur est un élément d'un espace vectoriel. Il peut être un n-uplet de , un polynôme, une fonction, une matrice, une suite ...

I Géométrie des vecteurs

II Coordonnées des points et des vecteurs dans un repère cartésien du plan

III Colinéarité, parallélisme

IV Produit scalaire, norme

I Géométrie des vecteurs

Vecteurs du plan → I Géométrie des vecteurs
Dans cette partie, après un rappel sur les parallélogrammes, nous donnons la définition d'un vecteur géométrique, des représentants d'un vecteur. Nous décrivons les opérations sur les vecteurs et nous établissons des correspondances entre vecteur et point.

I-1 Parallélogramme

I-2 Vecteur géométrique

I-3 Egalité de vecteurs géométriques

I-4 Vecteur, représentant

I-5 Opérations sur les vecteurs

I-6 Caractérisation vectorielle de points

Vecteurs du plan → I Géométrie des vecteurs

I-1 Parallélogramme

Vecteurs du plan → I Géométrie des vecteurs → I-1 Parallélogramme
Voici quelques propriétés des parallélogrammes, essentielles pour l'étude des vecteurs géométriques.

Définition

On dit que le quadrilatère (non aplati) A B C D est un parallélogramme si les droites (A B) et (C D) ainsi que (A D) et (B C) sont parallèles.

Proposition

Le quadrilatère (non aplati) A B C D est un parallélogramme si et seulement si ses diagonales [A C] et [B D] ont même milieu.

Proposition

Le quadrilatère (non aplati) convexe A B C D est un parallélogramme si et seulement si ses côtés opposés sont deux à deux de même longueur.
Sur la figure, les points B et C sont mobiles et permettent de changer l'allure du parallélogramme A B C D.
Vecteurs du plan → I Géométrie des vecteurs → I-1 Parallélogramme

I-2 Vecteur géométrique

Vecteurs du plan → I Géométrie des vecteurs → I-2 Vecteur géométrique

Définition

A tout couple de points distincts A et B du plan on associe un vecteur géométrique noté .
On dit que le vecteur géométrique a :
  • pour direction toute droite parallèle à (AB),
  • pour sens le sens de A vers B et
  • pour norme la longueur A B. La norme du vecteur se note : .
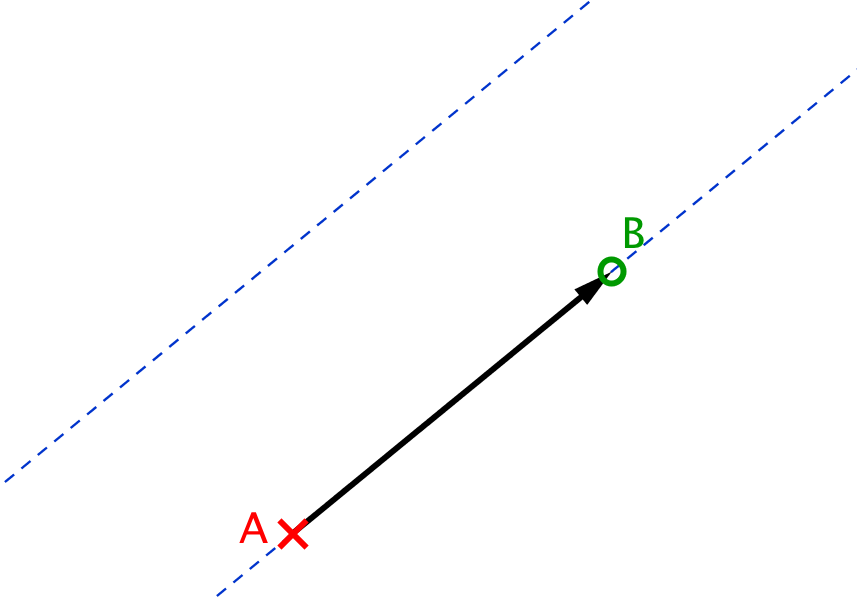
On dit que A est l'origine du vecteur et B l'extrémité du vecteur.
Sur la figure, le vecteur a pour direction la direction des droites en pointillées bleues qui sont parallèles.

Remarque

Le vecteur caractérise la translation du plan qui amène le point A vers le point B.

Exercice


direction, sens et norme.
Vecteurs du plan → I Géométrie des vecteurs → I-2 Vecteur géométrique

I-3 Egalité de vecteurs géométriques

Vecteurs du plan → I Géométrie des vecteurs → I-3 Egalité de vecteurs géométriques

I-3-1 Egalité entre vecteurs

I-3-2 Caractérisation géométrique de deux vecteurs égaux

Vecteurs du plan → I Géométrie des vecteurs → I-3 Egalité de vecteurs géométriques

I-3-1 Egalité entre vecteurs

Vecteurs du plan → I Géométrie des vecteurs → I-3 Egalité de vecteurs géométriques → I-3-1 Egalité entre vecteurs

Définition

  • Si les points A, B et C ne sont pas alignés, on dit que les vecteurs géométriques et sont égaux si le quadrilatère A B D C est un parallélogramme.
  • Si les points A, B et C sont alignés, on dit que les vecteurs géométriques et sont égaux s'il existe E et F deux points n'appartenant pas à (A B), tels que les vecteurs et (resp. et ) soient égaux.

I-3-2 Caractérisation géométrique de deux vecteurs égaux

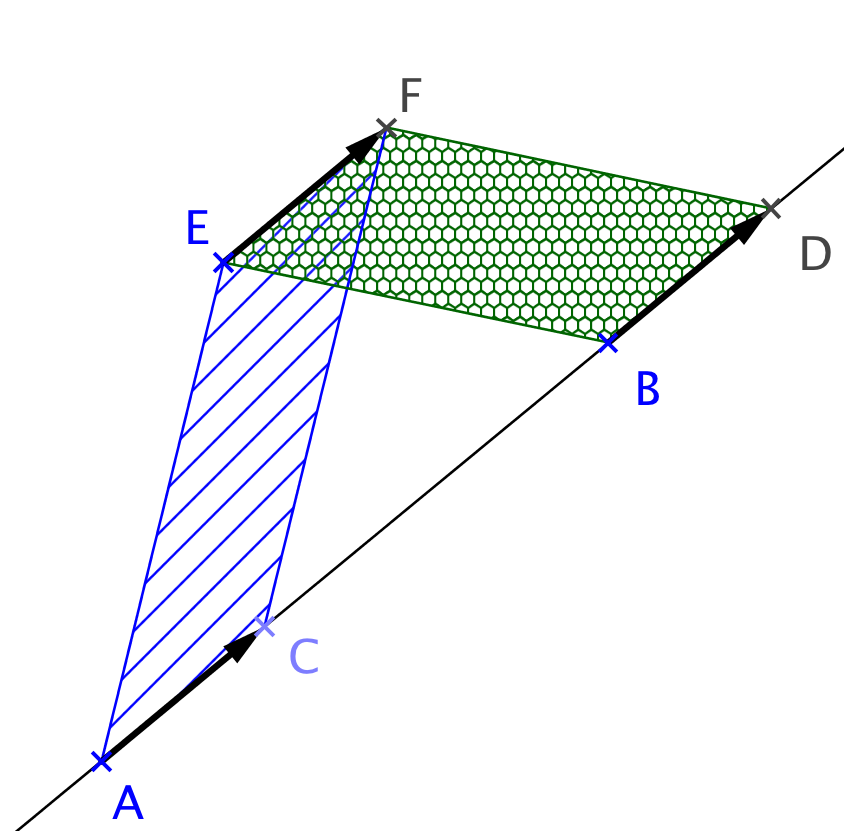
Vecteurs du plan → I Géométrie des vecteurs → I-3 Egalité de vecteurs géométriques → I-3-2 Caractérisation géométrique de deux vecteurs égaux

Définition

Soient deux vecteurs et de même direction, c'est-à-dire que (A C) et (B D) sont parallèles. On dit que et ont même sens si C et D se trouvent dans le même demi-plan limité par (A B).

Proposition

Deux vecteurs non nuls sont égaux si et seulement s'ils ont même direction, même sens et même norme.

Exercice

Egalité vectorielle
Vecteurs du plan → I Géométrie des vecteurs → I-3 Egalité de vecteurs géométriques → I-3-2 Caractérisation géométrique de deux vecteurs égaux

I-4 Vecteur, représentant

Vecteurs du plan → I Géométrie des vecteurs → I-4 Vecteur, représentant
Tous les vecteurs géométriques égaux sont les représentants d'un même vecteur (abstrait), noté en général par une seule lettre minuscule .
Si le vecteur a pour représentant , il admet une infinité de représentants : tous les vecteurs tels que A B B'A' soit un parallélogramme. Comme tous ces représentants de sont égaux, ils ont mêmes direction, sens et norme qui sont, par définition, ceux de .
Deux vecteurs abstraits et sont égaux s'il existe un représentant de et un représentant de tels que . De fait, et sont égaux s'ils ont mêmes direction, sens et norme.

Remarques

  • On voit ainsi qu'un vecteur n'est pas attaché à une origine. Ce sont ses représentants qui admettent chacun une origine et une extrémité.
  • Par abus, on écrit pour indiquer que le vecteur a pour représentant .

Définition [Vecteur nul]

Le vecteur nul est noté ; il a pour représentant pour tout point A du plan. Le vecteur nul n'a ni direction, ni sens. Sa norme est nulle.
Vecteurs du plan → I Géométrie des vecteurs → I-4 Vecteur, représentant

I-5 Opérations sur les vecteurs

Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs
Nous définissons la somme de deux vecteurs et la multiplication d'un vecteur par un réel. Ces opérations ne dépendent pas des représentants choisis.

I-5-1 Somme de deux vecteurs

I-5-2 Opposé d'un vecteur

I-5-3 Multiplication d'un vecteur par un réel

I-5-4 Règles du calcul vectoriel

Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs

I-5-1 Somme de deux vecteurs

Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs → I-5-1 Somme de deux vecteurs
On additionne deux vecteurs en utilisant soit la relation de Chasles, soit la règle du parallélogramme.

Définition [Relation de Chasles]

Pour tous points A, B et C du plan, on a :
Par la relation de Chasles, on additionne les vecteurs en les mettant bout à bout.

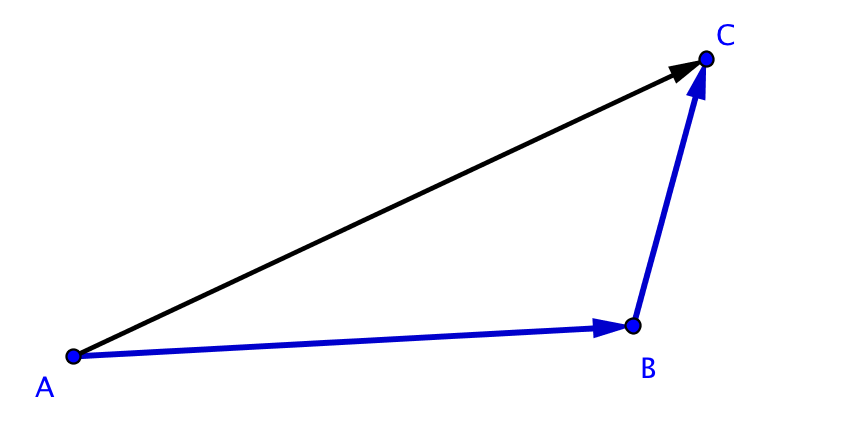
Définition [Règle du parallélogramme]

Pour trois points A, B et C du plan, notons D le point tel que A B D C soit un parallélogramme. Alors on a :
Par la règle du parallélogramme, on additionne des vecteurs de même origine.

Remarque


  • Les deux définitions sont compatibles puisque, comme les vecteurs et sont égaux dans le parallélogramme, le vecteur est aussi la somme par la relation de Chasles.
  • La somme d'un vecteur et du vecteur nul est le vecteur .

Exercices


Relation de Chasles
Somme graphique de deux vecteurs
Relations de Chasles dans des hexagones

I-5-2 Opposé d'un vecteur

Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs → I-5-2 Opposé d'un vecteur

Définition [Opposé d'un vecteur]

L'opposé du vecteur est le vecteur noté tel que la somme de et soit le vecteur nul.
L'opposé du vecteur nul est le vecteur nul : .

Proposition

  • Pour tous points A et B du plan, on a l'égalité : .
  • Si est un vecteur non nul, son opposé a même direction et même norme que , mais son sens est opposé à celui de .

I-5-3 Multiplication d'un vecteur par un réel

Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs → I-5-3 Multiplication d'un vecteur par un réel

Définition [Multiplication d'un vecteur par un réel]

Soit k un réel et un vecteur du plan. On note le vecteur défini comme suit :
  • Pour k=0 ou , on pose : ;
  • pour k > 0 et , le vecteur a la même direction que , le même sens que et sa norme vérifie : ;
  • pour k < 0 et , le vecteur a la même direction que , le sens opposé à et sa norme vérifie : .

Remarque

On retiendra la formule : où est la valeur absolue de k.
Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs → I-5-3 Multiplication d'un vecteur par un réel

I-5-4 Règles du calcul vectoriel

Vecteurs du plan → I Géométrie des vecteurs → I-5 Opérations sur les vecteurs → I-5-4 Règles du calcul vectoriel

L'addition, la soustraction et la multiplication par un réel de vecteurs suivent les mêmes règles de calcul que dans , sauf que l'on ne multiplie pas et que l'on ne divise pas deux vecteurs entre eux.

Proposition

Pour tous réels k et k', pour tous vecteurs , et , on a :

Remarque

On notera l'égalité .

Exercices


Relation entre trois vecteurs
Produit d'un vecteur par un réel

I-6 Caractérisation vectorielle de points

Vecteurs du plan → I Géométrie des vecteurs → I-6 Caractérisation vectorielle de points

Proposition

Soit un vecteur donné du plan et A un point donné du plan. Il existe un unique point M tel que .

Le vecteur est le vecteur géométrique d'origine A représentant de .

Remarque

Pour construire un point M défini par une égalité vectorielle, on se ramène à une égalité de la forme , où A est un point connu et un vecteur connu.

Voici quelques caractérisations de points ou figures remarquables et, pour apprendre à les reconnaître, un exercice :
Caractérisation vectorielle de propriétés géométriques

I-6-1 Milieu d'un segment

I-6-2 Centre de gravité d'un triangle

I-6-3 Parallélogramme

Vecteurs du plan → I Géométrie des vecteurs → I-6 Caractérisation vectorielle de points

I-6-1 Milieu d'un segment

Vecteurs du plan → I Géométrie des vecteurs → I-6 Caractérisation vectorielle de points → I-6-1 Milieu d'un segment

Proposition

Soient A et B deux points du plan. Le point I est le milieu de [AB] si et seulement l'une des propriétés équivalentes suivantes est vérifiée :
  • pour tout point M du plan,

I-6-2 Centre de gravité d'un triangle

Vecteurs du plan → I Géométrie des vecteurs → I-6 Caractérisation vectorielle de points → I-6-2 Centre de gravité d'un triangle

Proposition

Soient A, B et C trois points non alignés du plan. Les points A', B' et C' sont les milieux respectifs de [B C], [C A] et [A B]. Le point G est le centre de gravité du triangle ABC (càd le point d'intersection des trois médianes (A A'), (B B') et (C C')) si et seulement l'une des propriétés équivalentes suivantes est vérifiée :
  • .
  • .
  • .
  • .
  • Pour tout point M du plan, .
Sur la figure, quand on déplace les sommets du triangle le rapport reste égal à .

I-6-3 Parallélogramme

Vecteurs du plan → I Géométrie des vecteurs → I-6 Caractérisation vectorielle de points → I-6-3 Parallélogramme
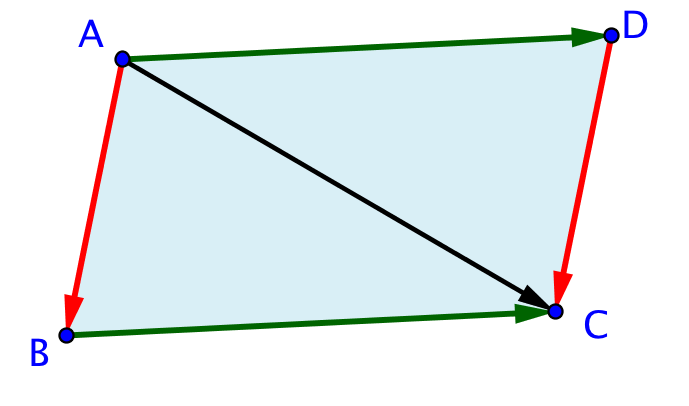
Des définitions données précédemment, on déduit ces caractérisations vectorielles d'un parallélogramme.

Proposition

Le quadrilatère (non aplati) A B C D est un parallélogramme si et seulement si l'une des propriétés équivalentes suivantes est vérifiée :
  • .
  • .
  • .

II Coordonnées des points et des vecteurs dans un repère cartésien du plan

Vecteurs du plan → II Coordonnées points et vecteurs
Après la définition géométrique des vecteurs, nous les présentons dans le cadre analytique.

II-1 Repère cartésien du plan

II-2 Coordonnées cartésiennes

II-3 Règles de calculs sur les coordonnées de vecteurs

II-4 Exemples et exercices

Vecteurs du plan → II Coordonnées points et vecteurs

II-1 Repère cartésien du plan

Vecteurs du plan → II Coordonnées points et vecteurs → II-1 Repère cartésien du plan
Une figure est disponible ici .

Définition

On définit un repère cartésien du plan par la donnée d'un point origine O et de deux vecteurs et non nuls et dont les directions ne sont pas parallèles, c'est-à-dire des vecteurs non colinéaires (voir ici ).
Quand les vecteurs et ont des directions perpendiculaires, on dit que le repère est orthogonal. Si de plus et sont de même norme, on dit que le repère est orthonormal (ou orthonormé).

Remarque

Le couple de vecteurs est la base du repère. Quand le repère est orthonormal, on dit que la base est orthonormale
Vecteurs du plan → II Coordonnées points et vecteurs → II-1 Repère cartésien du plan

II-2 Coordonnées cartésiennes

Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes
Dans un repère cartésien, un point ou un vecteur du plan est repéré par deux nombres, ses coordonnées.

II-2-1 Coordonnées cartésiennes d'un point

II-2-2 Coordonnées cartésiennes d'un vecteur

II-2-3 Exercices

Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes

II-2-1 Coordonnées cartésiennes d'un point

Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes → II-2-1 Coordonnées cartésiennes d'un point

Théorème


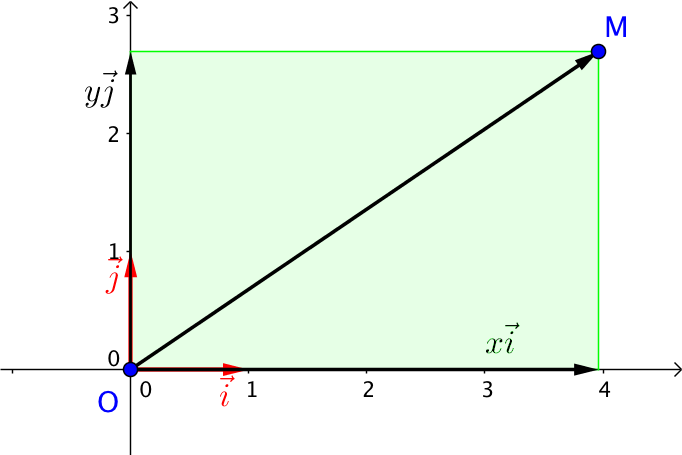
Le plan étant muni du repère , pour tout point M, il existe un unique couple de réels (x,y) tels que : .
On appelle (x,y), le couple de coordonnées cartésiennes de M. On dit que x est l'abscisse de M et que y est l'ordonnée de M. On note M(x,y) ; on lit M de coordonnées x et y .
Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes → II-2-1 Coordonnées cartésiennes d'un point

II-2-2 Coordonnées cartésiennes d'un vecteur

Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes → II-2-2 Coordonnées cartésiennes d'un vecteur

Théorème

Le plan étant muni du repère , pour tout vecteur , il existe un unique couple de réels tels que : .
On appelle , le couple de coordonnées cartésiennes de . On dit que est l'abscisse de et que est l'ordonnée de . On note ou ; on lit a pour coordonnées et .

Proposition

Deux vecteurs sont égaux si et seulement si leurs coordonnées sont égales.
Un vecteur est nul si et seulement si ses coordonnées sont nulles.
Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes → II-2-2 Coordonnées cartésiennes d'un vecteur

II-2-3 Exercices

Vecteurs du plan → II Coordonnées points et vecteurs → II-2 Coordonnées cartésiennes → II-2-3 Exercices

Exercices


Associer vecteurs et coordonnées
Lire les coordonnées d'un vecteur
Tracer un vecteur de coordonnées données
Placer l'origine ou l'extrémité d'un vecteur de coordonnées données

II-3 Règles de calculs sur les coordonnées de vecteurs

Vecteurs du plan → II Coordonnées points et vecteurs → II-3 Règles de calculs sur les coordonnées de vecteurs

Proposition

Dans le plan muni d'un repère, on considère des vecteurs et .
  • La somme des deux vecteurs a pour coordonnées
  • Le produit du vecteur par le réel k a pour coordonnées
  • Si a et b sont deux réels, le vecteur est une combinaison linéaire des vecteurs et . Ses coordonnées sont

Proposition

Soient deux points A (xA,ya) et B(xb,yb). Le vecteur a pour coordonnées cartésiennes .
Vecteurs du plan → II Coordonnées points et vecteurs → II-3 Règles de calculs sur les coordonnées de vecteurs

II-4 Exemples et exercices

Vecteurs du plan → II Coordonnées points et vecteurs → II-4 Exemples et exercices

Exercices


Coordonnées d'un vecteur défini par deux points
Somme graphique de deux vecteurs et coordonnées

Exemple [Calculer les coordonnées d'un point défini par une relation vectorielle]

Soient A un point donné et un vecteur donné. Soit M(x,y) le point du plan défini par la relation . Pour déterminer les coordonnées de M on résout le système suivant, d'inconnues x et y :

Exercices


Point défini par une origine et un vecteur
Coordonnées d'un point défini par une relation vectorielle
Combinaison linéaire graphique de deux vecteurs
Parallélogramme

Exemple [Milieu d'un segment]


Le point I milieu du segment [A B] a pour coordonnées : .

Exemple [Centre de gravité d'un triangle]


Le centre de gravité G d'un triangle A B C a pour coordonnées : .
Vecteurs du plan → II Coordonnées points et vecteurs → II-4 Exemples et exercices

III Colinéarité, parallélisme

Vecteurs du plan → III Colinéarité, parallélisme
Au parallélisme de deux droites correspond une relation linéaire entre des vecteurs portés par ces droites.

III-1 Définitions et propriétés

III-2 Critère de colinéarité sur les coordonnées

Vecteurs du plan → III Colinéarité, parallélisme

III-1 Définitions et propriétés

Vecteurs du plan → III Colinéarité → III-1 Définitions et propriétés

Définition [Vecteurs colinéaires]

On dit que deux vecteurs non nuls sont colinéaires s'ils ont la même direction. Par convention, le vecteur nul est colinéaire à tout autre vecteur.

Proposition

Les droites (A B) et (C D) sont parallèles si et seulement si les vecteurs et sont colinéaires. Trois points A, B et C sont alignés si et seulement les vecteurs et sont colinéaires.

Théorème

Soient et deux vecteurs non nuls. Les vecteurs et sont colinéaires si et seulement il existe un réel k tel que .
Vecteurs du plan → III Colinéarité → III-1 Définitions et propriétés

III-2 Critère de colinéarité sur les coordonnées

Vecteurs du plan → III Colinéarité → III-2 Critère de colinéarité sur les coordonnées
Voici le théorème précédent traduit sur les coordonnées :

Théorème

Dans le plan muni du repère , on considère et deux vecteurs non nuls de coordonnées respectives (x,y) et (x',y'). Les vecteurs et sont colinéaires si et seulement si leurs coordonnées sont proportionnelles, c'est-à-dire s'il existe un réel k tel que x' = k x et y' = k y.

Le critère de proportionnalité bien connu donne donc le critère de colinéarité suivant :

Théorème [Critère de colinéarité]

Dans le plan muni du repère , on considère et deux vecteurs non nuls de coordonnées respectives (x,y) et (x',y'). Les vecteurs et sont colinéaires si et seulement si on a l'égalité

Remarque

Le réel x y' - x'y est le produit en croix des coordonnées, il est aussi appelé déterminant de et et noté .

Exercices


Critère de colinéarité sur les coordonnées
Calcul d'un paramètre pour colinéarité
Alignement de 3 points
Vecteurs du plan → III Colinéarité → III-2 Critère de colinéarité sur les coordonnées

IV Produit scalaire, norme

Vecteurs du plan → IV Produit scalaire, norme
Dans cette partie, on associe un nombre à un couple de vecteurs, leur produit scalaire. Il permet de calculer la norme d'un vecteur et de caractériser l'orthogonalité, l'angle géométrique de deux vecteurs.
La définition d'un repère orthonormé est donnée ici .

IV-1 Produit scalaire

IV-2 Norme

IV-3 Angle géométrique de deux vecteurs

Vecteurs du plan → IV Produit scalaire, norme

IV-1 Produit scalaire

Vecteurs du plan → IV Produit scalaire → IV-1 Produit scalaire

Définition

Dans le plan muni d'un repère orthonormé, on considère deux vecteurs et de coordonnées respectives (x,y) et (x',y'). On définit leur produit scalaire par :

La proposition suivante précise les règles de calcul du produit scalaire, elle se démontre par le calcul ; elle signifie que le produit scalaire est une forme bilinéaire symétrique.

Proposition


Le produit scalaire est symétrique : Pour tous vecteurs et , on a : . Le produit scalaire est linéaire en chaque variable ; par symétrie, il suffit de l'écrire pour le premier vecteur.
  • Pour tout , pour tous vecteurs et , on a :
  • Pour tous , et , on a :

Exercice


Calcul de produit scalaire
Vecteurs du plan → IV Produit scalaire → IV-1 Produit scalaire

IV-2 Norme

Vecteurs du plan → IV Produit scalaire → IV-2 Norme

Proposition

Dans le plan muni d'un repère orthonormé, la norme du vecteur de coordonnées (x,y) est égale à la racine carrée de son carré scalaire et est notée .
La bilinéarité du produit scalaire permet de démontrer les formules suivantes dont on notera l'analogie avec des identités remarquables bien connues.

Proposition

Pour tous et , on a :

Exercices


Calcul utilisant la bilinéarité
Calcul de norme

IV-3 Angle géométrique de deux vecteurs

Vecteurs du plan → IV Produit scalaire → IV-3 Angle géométrique de deux vecteurs

Proposition

Soient A, B et C trois points distincts du plan muni d'un repère orthonormé. Le produit scalaire de et est égal à .
En particulier, les vecteurs et sont orthogonaux (voir ici ) si et seulement si leur produit scalaire est nul.

Exercices


Vecteurs orthogonaux ?
Vecteur normé colinéaire ou orthogonal
Produit scalaire et cosinus
Vecteurs du plan → IV Produit scalaire → IV-3 Angle géométrique de deux vecteurs

résumé accompagné d'exercices sur les vecteurs en géométrie plane.
: vectors,scalar_product, interactive mathematics, interactive math, server side interactivity

The most recent version
Cette page n'est pas dans son apparence habituelle parce que WIMS n'a pas pu reconnaître votre navigateur web.
Afin de tester le navigateur que vous utilisez, veuillez taper le mot wims ici : puis appuyez sur ``Entrer''.

Veuillez noter que les pages WIMS sont générées interactivement; elles ne sont pas des fichiers HTML ordinaires. Elles doivent être utilisées interactivement EN LIGNE. Il est inutile pour vous de les ramasser par un programme robot.